Exercício Resolvido de Movimento Unidimensional
publicidade
Um carro parte do repouso em Movimento Retilíneo Uniformemente Variado (M.R.U.V.). O carro percorre 100 m e 120 m em segundos sucessivos. Determinar a aceleração do movimento.
Dados do problema:
- Velocidade inicial do carro: v0 = 0;
- Distância percorrida entre t e (t +1) segundos: S2 − S1 = 100 m;
- Distância percorrida entre (t +1) e (t +2) segundos: S3 − S2 = 120 m.
Adotamos um sistema de referência orientado para a direita, o carro parte da origem, S0 = 0.
Após t segundos da partida o carro percorre uma distância de S metros. Então no intervalo de tempo de 1 segundo, entre t e (t+1) segundos, percorre o espaço de 100 metros chegando na posição (S+100) metros.
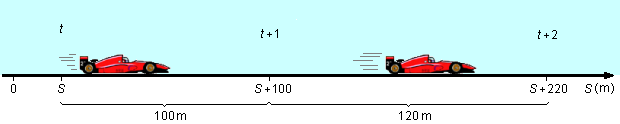
No próximo intervalo de tempo de 1 segundo, entre t+1 e t+2 segundos, percorre o espaço de 120 metros chegando na posição S+220 metros.
Solução
O carro está em Movimento Retilíneo Uniformemente Variado (M.R.U.V.), a equação deste movimento é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_{0}+v_{0}t+\frac{a}{2}t^{2}} \tag{I}
\end{gather}
\]
Escrevendo esta equação para o movimento do carro entre a origem S0 = 0 e o ponto S
\[
\begin{gather}
S=0+0.t+\frac{a}{2}t^{2}\\
S=\frac{a}{2}t^{2} \tag{II}
\end{gather}
\]
Escrevendo a expressão (I) para o movimento do carro entre a origem S0 = 0 e o ponto
S+100
\[
\begin{gather}
S+100=0+0.t+\frac{a}{2}(t+1)^{2}\\
S+100=\frac{a}{2}(t+1)^{2} \tag{III}
\end{gather}
\]
Escrevendo a expressão (I) para o movimento do carro entre a origem S0 = 0 e o ponto
S+220
\[
\begin{gather}
S+220=0+0.t+\frac{a}{2}(t+2)^{2}\\
S+220=\frac{a}{2}(t+2)^{2} \tag{IV}
\end{gather}
\]
As expressões (II), (III) e (IV) formam um sistema de três equações a três incógnitas S, a e
t
\[
\begin{gather}
\left\{
\begin{array}{l}
S=\dfrac{a}{2}t^{2}\\
S+100=\dfrac{a}{2}(t+1)^{2}\\
S+220=\dfrac{a}{2}(t+2)^{2}
\end{array}
\right. \tag{V}
\end{gather}
\]
subtraindo a primeira equação da segunda no sistema (V)
\[
\begin{gather}
\quad \cancel{S}+100=\frac{a}{2}(t+1)^{2}\\
\frac{\text{(-)} \qquad\quad \cancel{S}=\dfrac{a}{2}t^{2} \qquad\quad}{100=\dfrac{a}{2}(t+1)^{2}-\dfrac{a}{2}t^{2}}
\end{gather}
\]
colocando o termo
\( \frac{a}{2} \)
em evidência do lado direito da igualdade
\[
100=\frac{a}{2}\left[(t+1)^{2}-t^{2}\right]
\]
Lembrando dos Produtos Notáveis
\[
(a+b)^{2}=a^{2}+2ab+b^{2}
\]
desenvolvendo o primeiro termo entre colchetes
\[
\begin{gather}
100=\frac{a}{2}\left[t^{2}+2t+1-t^{2}\right]\\
100=\frac{a}{2}\left(2t+1\right) \tag{VI}
\end{gather}
\]
Subtraindo a segunda equação da terceira no sistema (V)
\[
\begin{gather}
\qquad\; \cancel{S}+220=\frac{a}{2}(t+2)^{2} \qquad \\
\frac{\text{(-)} \quad \cancel{S}+100=\dfrac{a}{2}(t+1)^{2} \qquad}{120=\dfrac{a}{2}(t+2)^{2}-\dfrac{a}{2}(t+1)^{2}}
\end{gather}
\]
colocando o termo
\( \frac{a}{2} \)
em evidência do lado direito da igualdade
\[
120=\frac{a}{2}\left[(t+2)^{2}-(t+1)^{2}\right]
\]
os dois termos entre colchetes são Produtos Notáveis da mesma forma usada acima
\[
\begin{gather}
120=\frac{a}{2}\left[t^{2}+2.2t+2^{2}-\left(t^{2}+2t+1\right)\right]\\
120=\frac{a}{2}\left[t^{2}+4t+4-t^{2}-2t-1\right]\\
120=\frac{a}{2}\left(2t+3\right) \tag{VII}
\end{gather}
\]
As expressões (VI) e (VII) formam um sistema de duas equações a duas incógnitas a e t
\[
\left\{
\begin{matrix}
100=\dfrac{a}{2}\left(2t+1\right)\\
120=\dfrac{a}{2}\left(2t+3\right)
\end{matrix} \tag{VIII}
\right.
\]
subtraindo a primeira equação da segunda no sistema (VIII)
\[
\frac{\left.
\begin{matrix}
\quad\quad 120=\dfrac{a}{2}\left(2t+3\right)\\
(-) \quad 100=\dfrac{a}{2}\left(2t+1\right)
\end{matrix} \quad
\right.}{20=\dfrac{a}{2}(2t+3)-\dfrac{a}{2}(2t+1)}
\]
colocando o termo
\( \frac{a}{2} \)
em evidência do lado direito da igualdade
\[
\begin{gather}
20=\frac{a}{2}\left[(2t+3)-(2t+1)\right]\\
20=\frac{a}{2}\left[2t+3-2t-1\right]\\
20=\frac{a}{\cancel{2}}.\cancel{2}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a=20\;\text{m/s}^{2}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .