Exercício Resolvido de Correntes Fictícias de Maxwell

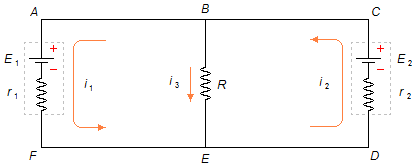
Duas pilhas cujas f.e.m. e resistências internas são respectivamente E₁=1,5 V, E₂=9 V e r₁=1 Ω, r₂=2,2 Ω são ligadas por fios de resistência desprezível a um resistor R=4,7 kΩ, segundo o esquema indicado na figura. Determinar as intensidades das correntes nos diferentes trechos do circuito.

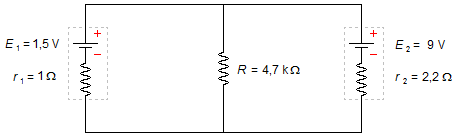
Dados do problema:

Resistores:

r₁ = 1 Ω;
r₂ = 2,2 Ω;

Resistência externa:

R = 4,7 kΩ = 4700 Ω;

f.e.m. das pilhas:

E₁ = 1,5 V;
E₂ = 9 V;

Solução:

Em primeiro lugar a cada malha do circuito atribuímos, aleatoriamente, um sentido de corrente. Na malha ABEFA temos a corrente i₁ no sentido horário, e na malha BCDEB temos a corrente i₂ no sentido anti-horário (Figura 1)

Figura 1

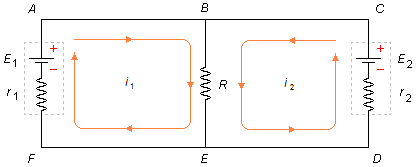
Aplicando a Lei das Malhas à malha i₁ a partir do ponto A no sentindo escolhido, esquecendo a malha i₂ (Figura 2)

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_n V_n=0} \end{gather} \]

\[ \begin{gather} R(i_1+i_2)+r_1i_1-E_1=0 \end{gather} \]

Figura 2

substituindo os valores do problema fica

\[ \begin{gather} 4700(i_1+i_2)+1i_1-1,5=0 \\[5pt] 4700i_1+4700i_2+i_1=1,5 \\[5pt] {4701i_1+4700i_2=1,5 \tag{I}} \end{gather} \]

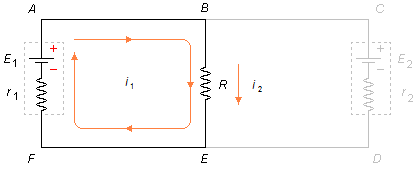
Aplicando a Lei das Malhas à malha i₂ a partir do ponto B no sentindo escolhido, esquecendo a malha i₁ (Figura 3)

\[ \begin{gather} R(i_1+i_2)+r_2i_2-E_2=0 \end{gather} \]

Figura 3

substituindo os valores do problema fica

\[ \begin{gather} 4700(i_1+i_2)+2,2i_2-9=0 \\[5pt] 4700i_1+4700i_2+2,2i_2=9 \\[5pt] {4700i_1+4702,2i_2=9 \tag{II}} \end{gather} \]

Com as equações (I) e (II) temos um sistema de duas equações a duas incógnitas (i₁ e i₂)

\[ \begin{gather} \left\{ \begin{array}{l} \;4701i_1+4700i_2=1,5 \\ \;4700i_1+4702,2i_2=9 \end{array} \right. \end{gather} \]

isolando o valor de i₂ na primeira equação

\[ \begin{gather} i_2=\frac{1,5-4701i_1}{4700} \tag{III} \end{gather} \]

substituindo este valor na segunda equação

\[ \begin{gather} 4700i_1+4702,2\;\left(\frac{1,5-4701i_1}{4700}\;\right)=9 \end{gather} \]

multiplicando ambos os lados da igualdade pro 4700

\[ \begin{gather} 4700\times 4700i_1+4700\times 4702,2\;\left(\frac{1,5-4701i_1}{4700}\;\right)=4700\times 9 \\[5pt] 22090000i_1+\cancel{4700}\times 4702,2\;\left(\frac{1,5-4701i_1}{\cancel{4700}}\;\right)=4700\times 9 \\[5pt] 22090000i_1+4702,2\times 1,5-4702,2\times 4701i_1=42300 \\[5pt] 22090000i_1+7053,3-2210542,2i_1=42300 \\[5pt] -15042,2i_1=42300-7053,3 \\[5pt] -15042,2i_1=35246,7 \\[5pt] i_1=\frac{35246,7}{-15042,2} \\[5pt] i_1=-2,34319\;\mathrm A \end{gather} \]

Substituindo este valor na equação (III

\[ \begin{gather} i_2=\frac{1,5-4701\times(-2,34319)}{4700} \\[5pt] i_2=\frac{1,5+11015,33619}{4700} \\[5pt] i_2=\frac{11016,83619}{4700} \\[5pt] i_2=2,34401\;\mathrm A \end{gather} \]

No ramo BE vai circular uma corrente i₃ dada por

\[ \begin{gather} i_3=i_1+i_2 \\[5pt] i_3=-2,34319+2,34401 \\[5pt] i_3=0,00082=0,82\times 10^{-3}=0,82\;\mathrm{mA} \end{gather} \]

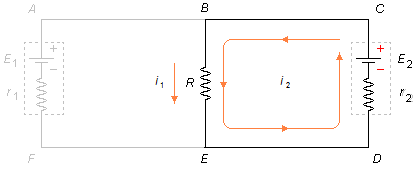
O sentido da corrente i₃ será o mesmo da corrente i₂ (de maior valor absoluto).
Como o valor da corrente i₁ é negativa, isto indica que seu verdadeiro sentido é contrário ao escolhido na Figura 1. Os valores das correntes são i₁=2,3432 A, i₂=2,3440 A, e i₃=0,82 mA, e seus sentidos estão mostrados na Figura 4.

Figura 4