Exercício Resolvido de Movimento Unidimensional
publicidade
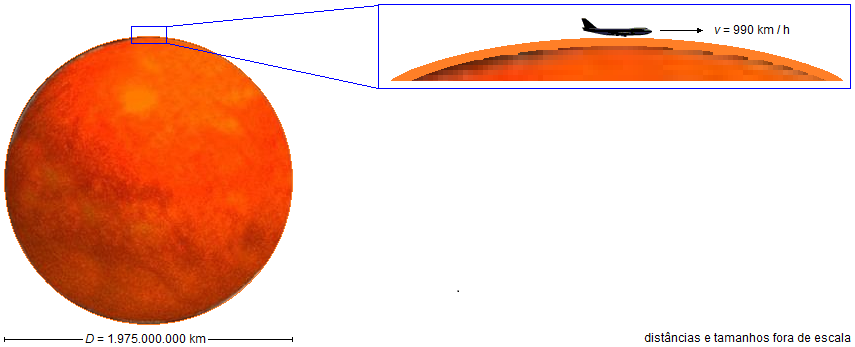
A maior estrela conhecida (até junho de 2019) é VY Canis Majoris na constelação do Cão Maior, com um diâmetro estimado em 1.975.000.000 km. Fazendo a suposição (absurda) de que um jato comercial pudesse voar rente a superfície da estrela a uma velocidade constante de 990 km/h. Quanto tempo levaria o jato para dar uma volta na estrela?. Dê a resposta em anos.
Dados do problema:
- Diâmetro da estrela: D = 1.975.000.000 km;
- Velocidade do jato: v = 990 km/h.
Solução
A distância que o avião deverá percorrer é a circunferência da estrela. O comprimento de uma circunferência é dado por
\[
\begin{gather}
C=2\pi r
\end{gather}
\]
onde, r é o raio da circunferência, o diâmetro D de uma circunferência igual a 2r, o
comprimento de uma circunferência também pode ser calculado por
\[
\begin{gather}
C=\pi D
\end{gather}
\]
usando π = 3,14 a circunferência da estrela será
\[
\begin{gather}
C=3,14\times 1975000000\\[5pt]
C=6201500000\;\mathrm{km}
\end{gather}
\]
Como a velocidade do avião é constante, temos que tempo da viagem é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
\[
\begin{gather}
\Delta t=\frac{\Delta S}{v}
\end{gather}
\]
usando o valor da velocidade dado no problema e sendo a distância igual ao comprimento da circunferência
calculado acima
\[
\begin{gather}
\Delta t=\frac{6201500000}{990}\\[5pt]
\Delta t=6264141\;\mathrm{h}
\end{gather}
\]
Convertendo este valor para anos como pede o problema
\[
\begin{gather}
\Delta t=6264141\;\cancel{\mathrm{horas}}\times\frac{1\;\cancel{\mathrm{dia}}}{24\;\cancel{\mathrm{horas}}}\times\frac{1\;\mathrm{ano}}{365\;\cancel{\mathrm{dias}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta t=715\;\mathrm{anos}}
\end{gather}
\]
Observação: para fazer comparação, o Sol tem 1.391.000 km de diâmetro, nessas mesmas
condições, o avião levaria "apenas" 184 dias para dar uma volta em torno do Sol.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .