Exercice Résolu sur les Mouvement Unidimensionnel
publicité
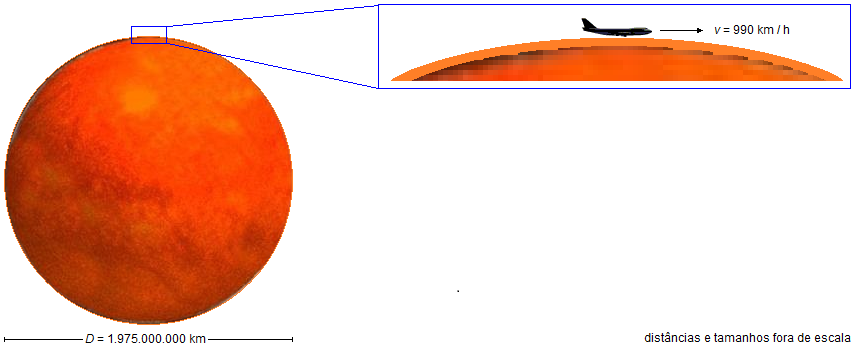
La plus grande étoile connue (jusqu'à juin 2019) est VY Canis Majoris dans la constellation du Grand Chien, avec un diamètre estimé de 1 975 000 000 km. En supposant (de manière absurde) qu'un avion de ligne puisse voler au ras de la surface de l'étoile à une vitesse constante de 990 km/h. Combien de temps faudrait-il à l'avion pour faire le tour de l'étoile ? Donnez la réponse en années.
Données du problème:
- Diamètre de l'étoile: D = 1.975.000.000 km;
- Vitesse de l'avion: v = 990 km/h.
Solution
La distance que l'avion devra parcourir est la circonférence de l'étoile. La longueur d'une circonférence est donnée par
\[
\begin{gather}
C=2\pi r
\end{gather}
\]
où r est le rayon de la circonférence, le diamètre D d'une circonférence étant égal à
2r, la longueur d'une circonférence peut également être calculée par
\[
\begin{gather}
C=\pi D
\end{gather}
\]
en utilisant π = 3,14 la circonférence de l'étoile sera
\[
\begin{gather}
C=3,14\times 1975000000\\[5pt]
C=6201500000\;\mathrm{km}
\end{gather}
\]
Comme la vitesse de l'avion est constante, nous avons que le temps du voyage est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\frac{\Delta S}{\Delta t}}
\end{gather}
\]
\[
\begin{gather}
\Delta t=\frac{\Delta S}{v}
\end{gather}
\]
en utilisant la valeur de la vitesse donnée dans le problème et la distance étant égale à la longueur de la
circonférence calculée ci-dessus
\[
\begin{gather}
\Delta t=\frac{6201500000}{990}\\[5pt]
\Delta t=6264141\;\mathrm{h}
\end{gather}
\]
En convertissant cette valeur en années comme le demande le problème
\[
\begin{gather}
\Delta t=6264141\;\cancel{\mathrm{horas}}\times\frac{1\;\cancel{\mathrm{dia}}}{24\;\cancel{\mathrm{horas}}}\times\frac{1\;\mathrm{anẽe}}{365\;\cancel{\mathrm{dias}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\Delta t=715\;\mathrm{anées}}
\end{gather}
\]
Remarque: pour comparaison, le Soleil a un diamètre de 1.391.000 km, dans ces mêmes
conditions, l'avion mettrait "seulement" 184 jours pour faire le tour du Soleil.
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .