Exercício Resolvido de Movimento Unidimensional
publicidade   



Dois barcos partem de um mesmo ponto, e se deslocam sobre a uma mesma reta, com velocidades constantes de 25 km/h e 35 km/h. A comunicação entre os dois barcos é possível, pelo rádio, enquanto a distância entre eles não ultrapassar 600 km. Determinar o tempo durante o qual os dois barcos podem se comunicar, admitindo que:
a) Os dois barcos movem-se no mesmo sentido;
b) O barco mais lento parte duas horas antes do outro e move-se no mesmo sentido;
c) Os dois barcos partem ao mesmo tempo e movem-se em sentidos opostos.


Dados do problema:
  • Velocidade do barco 1:    v1 = 25 km/h;
  • Velocidade do barco 2:    v2 = 35 km/h;
  • Distância máxima de comunicação:    Δt = 600 km.
Esquema do problema:

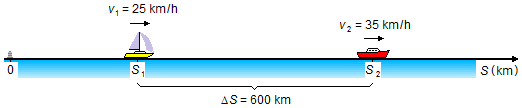
Adotamos um sistema de referência com o eixo positivo orientado para a direita (Figura 1).

Figura 1

Considerando o ponto de onde partem os barcos é a origem do referencial S01 = S02 = 0

Solução

a) Os barcos movem-se com velocidades constantes, estão em Movimento Retilíneo Uniforme (M.R.U.), dado por
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt} \end{gather} \]
escrevendo essa equação para cada um dos barcos
\[ \begin{gather} S_1=S_{01}+v_1 t\\[5pt] S_1=0+25t\\[5pt] S_1=25t \tag{I-a} \end{gather} \]
\[ \begin{gather} S_2=S_{02}+v_2 t\\[5pt] S_2=0+35t\\[5pt] S_2=35t \tag{I-b} \end{gather} \]
O barco 2 de maior velocidade se afasta do barco 1 até que distância entre os dois seja maior que 600 km e a comunicação deixa de ser possível (Figura 2).

Figura 2

Calculando a diferença entre as equações (I-a) e (I-b)
\[ \begin{gather} \frac{ \begin{align} \qquad\quad S_2 &=35t\\ \mathrm{(-)}\qquad S_1 &=25t \end{align} } {S_2-S_1=35t-25t} \end{gather} \]
Sendo ΔS = S2 − S1 = 600 km
\[ \begin{gather} \Delta S=10t\\[5pt] 10t=600\\[5pt] t=\frac{600}{10} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t=60\;\mathrm h} \end{gather} \]

b) O barco 1 parte e navega por 2 horas se afastando do ponto de partida, enquanto o barco 2 permanece parado. Durante este intervalo de tempo a comunicação entre os dois barcos é possível. Quando o barco 1 atinge uma posição S1, o barco 2 parte da origem, e navega até ultrapassar o barco 1, se afastando até que a distância entre eles seja maior que 600 km e a comunicação deixe de ser possível (Figura 3).

Figura 3

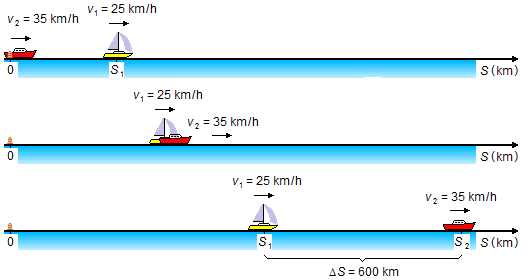
Sendo t o tempo de deslocamento do barco 2 o tempo de deslocamento do barco 1 será t+2 indicando que ele tem duas horas a mais de viagem, escrevendo as equações de movimento
\[ \begin{gather} S_1=S_{01}+v_1(t+2)\\[5pt] S_1=0+25(t+2)\\[5pt] S_1=25(t+2) \tag{II-a} \end{gather} \]
\[ \begin{gather} S_2=S_{02}+v_2 t\\[5pt] S_2=0+35t\\[5pt] S_2=35t \tag{II-b} \end{gather} \]
Calculando a diferença entre as duas expressões (II-a) e (II-b)
\[ \begin{gather} \frac{ \begin{align} S_2 &=35t\\ \mathrm{(-)}\qquad S_1 &=25(\;t+2\;) \end{align} } {S_2-S_1=35t-25(t+2)}\\[5pt] \Delta S=35t-25t-50\\[5pt] 10t=600+50\\[5pt] t=\frac{650}{10} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t=65\;\mathrm h} \end{gather} \]

c) Vamos adotar que o barco 1 parte no sentido contrário à orientação da trajetória, sua velocidade será negativa (v1=−25 km/h - Figura 4).

Figura 4

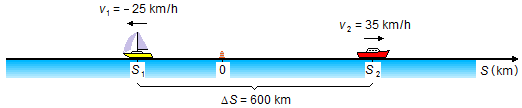
As equações desse movimento para os dois barcos serão
\[ \begin{gather} S_1=S_{01}+v_1 t\\[5pt] S_1=0-25t\\[5pt] S_1=-25t \tag{III-a} \end{gather} \]
\[ \begin{gather} S_2=S_{02}+v_2 t\\[5pt] S_2=0+35t \\[5pt] S_2=35t \tag{III-b} \end{gather} \]
Calculando a diferença entre as duas equações (III-a) e (III-b)
\[ \begin{gather} \frac{ \begin{align} S_2 &=35t\\ \mathrm{(-)}\qquad S_1 &=-25t \end{align} } {S_2-S_1=35t+25t}\\[5pt] \Delta S=60t\\[5pt] 60t=600\\[5pt] t=\frac{600}{60} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {t=10\;\mathrm h} \end{gather} \]
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .