Exercício Resolvido de Dinâmica

Em um dia sem vento um automóvel se desloca a uma velocidade constante de 72 km/h, o coeficiente de forma c igual a 0,6 unidades S.I. (Sistema Internacional de Unidades) e a área perpendicular à direção do movimento é de 3 m². Determine o módulo da força de resistência do ar.

Dados do problema:

Velocidade do automóvel: v = 72 km/h;
Coeficiente de forma: c = 0,6 S.I.;
Área da seção transversal: A = 3 m².

Esquema do problema:

Na Figura 1 são mostrados os elementos dados no problema e a força de resistência do ar \( {\vec F}_r \) a ser calculada.

Figura 1

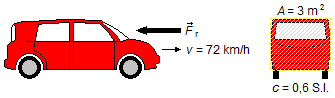
Solução:

Em primeiro lugar devemos converter a velocidade do carro dada em quilômetros por hora (km/h) para metros por segundo (m/s) usada no Sistema Internacional de Unidades (S.I.)

\[ \begin{gather} v=72\;\frac{\mathrm{\cancel{km}}}{\mathrm{\cancel h}}\times\frac{1000\;\mathrm m}{1\;\mathrm{\cancel{km}}}\times\frac{1\;\mathrm{\cancel h}}{3600\;\mathrm s}=\frac{72}{3,6}\;\frac{\mathrm m}{\mathrm s}=20\;\mathrm{m/s} \end{gather} \]

O módulo da força de resistência do ar é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {F_r=Kv^2} \tag{I} \end{gather} \]

onde K é o coeficiente aerodinâmico dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {K=cA} \tag{II} \end{gather} \]

substituindo a equação (II) na equação (I)

\[ \begin{gather} F_r=cAv^2 \\[5pt] F_r=0,6\times 3\times 20^2 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {F_r=720\;\mathrm N} \end{gather} \]

Observação: o módulo da força de resistência é dado por

\[ \begin{gather} F_r=\frac{1}{2}c_r\mu Av^2 \end{gather} \]

onde c_r é o coeficiente aerodinâmico, μ a densidade do ar, A a área transversal e v a velocidade. O coeficiente aerodinâmico é uma grandeza adimensional.
Neste problema a termo K foi chamado de coeficiente aerodinâmico, e depende de outra constante c chamada de coeficiente de forma

\[ \begin{gather} F_r=\underbrace{\overbrace{\frac{1}{2}c_r\mu}^{c}A}_{K}v^2 \end{gather} \]

Neste caso a constante K possui dimensão de massa por comprimento, \( \mathrm{M L^{-1}=\frac{kg}{m}} \)

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .