Exercício Resolvido de Dinâmica
publicidade   



No sistema da figura, o corpo A desliza sobre um plano horizontal sem atrito, arrastado por B que desce verticalmente. A e B estão presos entre si por uma corda inextensível de massa desprezível paralela ao plano e que passa pela polia de massa desprezível sem atrito. As massas de A e B valem respectivamente 32 kg e 8 kg. Determinar a aceleração do conjunto e a intensidade da força de tensão na corda.


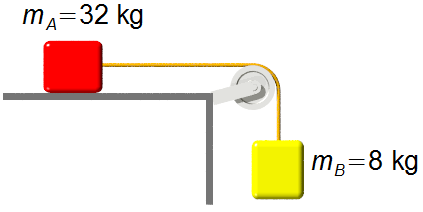
Dados do problema:
  • Massa do corpo A:    mA = 32 kg;
  • Massa do corpo B:    mB = 8 kg;
  • Aceleração da gravidade:    g = 9,8 m/s2.
Esquema do problema:

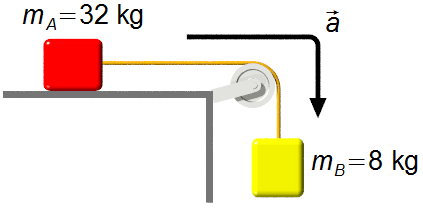
Adotamos um sistema de referência orientado para a direita no mesmo sentido da aceleração.
Figura 1

Fazendo um Diagrama de Corpo Livre temos as forças que atuam nos blocos.

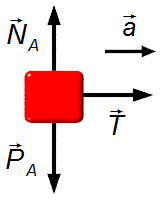
  • Corpo A (Figura 2):
    • Direção vertical:
      • \( \vec P_{\small A} \): peso do corpo A;
      • \( \vec N_{\small A} \): força de reação normal da superfície no corpo.
    • Direção horizontal:
      • \( \vec T \): força de tensão na corda.
Figura 2

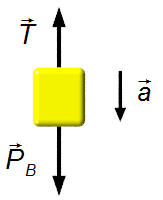
  • Corpo B (Figura 3):
    • \( \vec P_{\small B} \): peso do corpo B;
    • \( \vec T \): força de tensão na corda.
Figura 3

Solução

Aplicando a 2.ª Lei de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Corpo A:
Na direção vertical o peso e a normal se anulam.
Na direção horizontal
\[ \begin{gather} T=m_{\small A}a \tag{I} \end{gather} \]
  • Corpo B:
Na direção horizontal não há forças atuando.
Na direção vertical
\[ \begin{gather} P_{\small B}-T=m_{\small B}a \tag{II} \end{gather} \]
A força peso é dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]
para o corpo B
\[ \begin{gather} P_{\small B}=m_{\small B}g \tag{III} \end{gather} \]
substituindo a equação (III) na equação (II)
\[ \begin{gather} m_{\small B}g-T=m_{\small B}a \tag{IV} \end{gather} \]
As equações (I) e (IV) formam um sistema de duas equações a dua incógnitas (T e a), somando as duas equações
\[ \begin{gather} \frac{ \left\{ \begin{array}{rr} \cancel{T}&=m_{\small A}a\\ m_{\small B}g-\cancel{T}&=m_{\small B}a \end{array} \right.} {m_{\small B}g=\left(m_{\small A}+m_{\small B}\right)a}\\[5pt] a=\frac{m_{\small B}g}{m_{\small A}+m_{\small B}}\\[5pt] a=\frac{8\times 9,8}{32+8} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a\approx 1,9\;\mathrm{m/s^2}} \end{gather} \]
Substituindo a massa do corpo A e a aceleração, encontrada acima, na primeira equação do sistema a tensão na corda será
\[ \begin{gather} T=32\times 1,9 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T\approx 62,7\;\mathrm N} \end{gather} \]
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .