Ejercicio Resuelto sobre Campo Eléctrico
EN
FR
PT-BR
publicidad
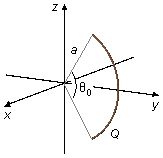
Un arco de circunferencia de radio a y ángulo central θ0 está cargado con
una carga Q distribuida uniformemente a lo largo del arco. Determine:
a) El vector campo eléctrico en los puntos de la recta que pasa por el centro del arco y es perpendicular al plano que contiene el arco;
b) El vector campo eléctrico en el centro de curvatura del arco;
c) El vector campo eléctrico cuando el ángulo central tiende a cero.
a) El vector campo eléctrico en los puntos de la recta que pasa por el centro del arco y es perpendicular al plano que contiene el arco;
b) El vector campo eléctrico en el centro de curvatura del arco;
c) El vector campo eléctrico cuando el ángulo central tiende a cero.
Datos del problema:
- Radio del arco: a;
- Ángulo central del arco: θ0;
- Carga eléctrica del arco: Q.
El vector posición r va de un elemento de carga dq del arco hasta el punto P, donde queremos calcular el campo eléctrico; el vector rq localiza el elemento de carga con respecto al origen del referencial y el vector rp localiza el punto P (Figura 1-A).
\[
\begin{gather}
\mathbf r=\mathbf r_p-\mathbf r_q
\end{gather}
\]
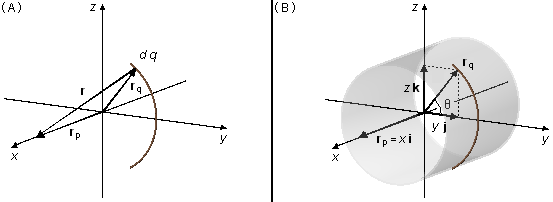
Por la geometría del problema, debemos elegir coordenadas cilíndricas (Figura 1-B); el vector rq, que está en el plano yz, se escribe como \( \mathbf r_q=y\;\mathbf j+z\;\mathbf k \) el vector rp solo tiene componente en la dirección i, \( \mathbf r_p=x\;\mathbf i \) (al contrario de lo que se hace usualmente, donde el vector rq está en el plano xy y el eje del cilindro en la dirección k); el vector posición será
\[
\begin{gather}
\mathbf r=x\;\mathbf i-\left(y\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf r=x\;\mathbf i-y\;\mathbf j-z\;\mathbf k \tag{I}
\end{gather}
\]
De la ecuación (I), el módulo del vector posición r será
\[
\begin{gather}
r^2=x^2+(-y)^2+(-z)^2\\[5pt]
r=\left(x^2+y^2+z^2\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
donde x, y y z, en coordenadas cilíndricas, se dan por
\[
\begin{gather}
\left\{
\begin{array}{l}
x=x\\
y=a\cos\theta\\
z=a\operatorname{sen}\theta
\end{array}
\right. \tag{III}
\end{gather}
\]
Solución:
a) El vector campo eléctrico está dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{dq}{r^2}\;\frac{\mathbf r}{r}}}
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{dq}{r^{3}}\;\mathbf r} \tag{IV}
\end{gather}
\]
Usando la ecuación de la densidad lineal de carga λ, obtenemos el elemento de carga dq
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\lambda=\frac{dq}{ds}}
\end{gather}
\]
\[
\begin{gather}
dq=\lambda\;ds \tag{V}
\end{gather}
\]
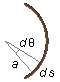
donde ds es un elemento de arco de ángulo dθ del arco (Figura 2)
\[
\begin{gather}
ds=a\;d\theta \tag{VI}
\end{gather}
\]
sustituyendo la ecuación (VI) en la ecuación (V)
\[
\begin{gather}
dq=\lambda a\;d\theta \tag{VII}
\end{gather}
\]
Sustituyendo las ecuaciones (I), (II) y (VII) en la ecuación (IV)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[\left(x^2+y^2+z^2\right)^{1/2}\right]^{\;3}}}\left(x\;\mathbf i-y\;\mathbf j-z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left(x^2+y^2+z^2\right)^{3/2}}}\left(x\;\mathbf i-y\;\mathbf j-z\;\mathbf k\right) \tag{VIII}
\end{gather}
\]
sustituyendo las ecuaciones de (III) en la ecuación (VIII)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[\;x^2+\left(a\cos\theta\right)^2+\left(a\operatorname{sen}\theta\right)^2\right]^{3/2}}}\left(x\;\mathbf i-a\cos\theta\;\mathbf j-a\operatorname{sen}\theta\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[x^2+a^2\cos^2\theta +a^2\operatorname{sen}^2\theta\;\right]^{3/2} }}\left(x\;\mathbf i-a\cos\theta\;\mathbf j-a\operatorname{sen}\theta\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[x^2+a^2\underbrace{\left(\cos ^2\theta+\operatorname{sen}^2\theta\right)}_{1}\right]^{3/2}}\left(x\;\mathbf i-a\cos\theta\;\mathbf j-a\operatorname{sen}\theta\;\mathbf k\right)}\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left(x^2+a^2\right)^{3/2}}\left(x\;\mathbf i-a\cos\theta\;\mathbf j-a\operatorname{sen}\theta\;\mathbf k\right)}
\end{gather}
\]
La densidad de carga λ y el radio a son constantes, por lo que pueden salir de la
integral, y la integral de la suma es igual a la suma de las integrales
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(x^2+a^2\right)^{3/2}}\left(x\int d\theta\;\mathbf i-a\int \cos\theta d\theta\;\mathbf j-a\int \operatorname{sen}\theta\;d\theta\;\mathbf k\right)
\end{gather}
\]
Como existe simetría, podemos dividir el ángulo central θ0 en dos partes midiendo
\( \frac{\theta_0}{2} \)
en el sentido horario y
\( -{\frac{\theta_0}{2}} \)
en el sentido antihorario (Figura 3), los límites de integración serán
\( -{\frac{\theta_0}{2}} \)
y
\( \frac{\theta_0}{2} \).
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(x^2+a^2\right)^{3/2}}\left(x\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}d\theta\;\mathbf i-a\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\cos\theta\;d\theta\;\mathbf j-a\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\operatorname{sen}\theta\;d\theta\;\mathbf k\right)
\end{gather}
\]
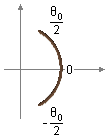
Figura 3
Integral de \( \displaystyle \int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\;d\theta \)
\[
\begin{align}
\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\;d\theta &=\frac{\theta_0}{2}-\left(-{\frac{\theta_0}{2}}\right)=\\
&=\frac{\theta_0}{2}+\frac{\theta_0}{2}=\cancel 2\frac{\theta_0}{\cancel 2}=\theta_0
\end{align}
\]
Integral de \( \displaystyle \int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\cos\theta\;d\theta \)
\[
\begin{align}
\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\cos\theta\;d\theta &=\left.\operatorname{sen}\theta\right|_{\;-\frac{\theta_0}{2}}^{\;\frac{\theta_0}{2}}=\\
&=\operatorname{sen}\frac{\theta_0}{2}-\operatorname{sen}\;\left(-{\frac{\theta_0}{2}}\right)
\end{align}
\]
la función seno es una función impar
\( f(-x)=-f(x) \),
\( \operatorname{sen}\left(-{\dfrac{\theta_0}{2}}\right)=-\operatorname{sen}\dfrac{\theta_0}{2} \)
\[
\begin{align}
\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\cos\theta\;d\theta &=\operatorname{sen}\frac{\theta_0}{2}-\left[-\operatorname{sen}\;\frac{\theta_0}{2}\right]=\\
&=\operatorname{sen}\frac{\theta_0}{2}+\operatorname{sen}\frac{\theta_0}{2}=2\;\operatorname{sen}\;\frac{\theta_0}{2}
\end{align}
\]
Integral de \( \displaystyle \int_{-{\frac{\theta_{;0}}{2}}}^{{\frac{\theta_{0}}{2}}}\operatorname{sen}\theta\;d\theta\)
\[
\begin{align}
\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\operatorname{sen}\theta\;d\theta &=\left.-\cos\theta\right|_{\;-\frac{\theta_0}{2}}^{\;\frac{\theta_0}{2}}=\\
&=-\left[\cos\frac{\theta_0}{2}-\cos\left(-{\frac{\theta_0}{2}}\right)\right]
\end{align}
\]
la función coseno es una función par
\( f(x)=f(-x) \),
\( \cos\left(-{\dfrac{\theta_0}{2}}\right)=\cos\dfrac{\theta_0}{2} \)
\[
\begin{gather}
\int_{-{\frac{\theta_0}{2}}}^{{\frac{\theta_0}{2}}}\operatorname{sen}\theta\;d\theta=-\left[\cos\frac{\theta_0}{2}-\cos\frac{\theta_0}{2}\right]=0
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(x^2+a^2\right)^{3/2}}\left(x\theta_0\;\mathbf i-2a\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j-0\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(x^2+a^2\right)^{3/2}}\left(x\theta_0\;\mathbf i-2a\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j\right) \tag{IX}
\end{gather}
\]
Observación: la integral en la dirección k es igual a cero, porque un elemento de
carga dq produce en un punto un elemento del campo que puede descomponerse en elementos
dEx, −dEy y
−dEz (Figura 4-A). Otro elemento de carga colocado en una posición
simétrica produce, en el mismo punto, otro elemento del campo que puede descomponerse en elementos
dEx, −dEy y
dEz (Figura 4-B), así los elementos en la dirección k se anulan y
solo los elementos en las direcciones i y j contribuyen al campo total.
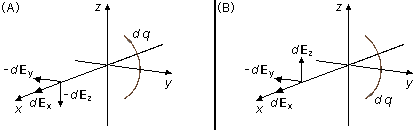Figura 4
La carga total del arco es Q y su longitud es aθ0. la densidad lineal de carga puede escribirse como
\[
\begin{gather}
\lambda=\frac{Q}{a\theta_0} \tag{X}
\end{gather}
\]
sustituyendo la ecuación (X) en la ecuación (IX)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{Q}{a\theta_0}\frac{a}{\left(x^2+a^2\right)^{3/2}}\left(x\theta_0\;\mathbf i-2a\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{Q}{\left(x^2+a^2\right)^{3/2}}\left(\frac{1}{\theta_0}x\theta_0\;\mathbf i-\frac{1}{\theta_0}2a\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{Q}{\left(x^2+a^2\right)^{3/2}}\left(x\;\mathbf i-\frac{2a}{\theta_0}\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j\right)}
\end{gather}
\]
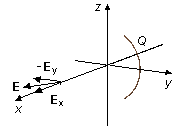
b) En el centro de curvatura tenemos x = 0, sustituyendo en la solución del ítem anterior (Figura 6)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{Q}{\left(0^2+a^2\right)^{3/2}}\left(0\;\mathbf i-\frac{2a}{\theta_0}\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j\right)\\[5pt]
\mathbf E=\frac{-{1}}{4\pi\epsilon_0}\frac{Q}{a^{3}}\frac{2a}{\theta_0}\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{-{1}}{4\pi\epsilon_0}\frac{Q}{a^2}\frac{2}{\theta_0}\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j}
\end{gather}
\]
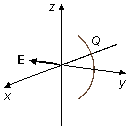
c) Cuando el ángulo central tiende a cero (\( \theta_0\rightarrow 0 \)), el arco tiende a una carga puntual; aplicando el límite a la solución del ítem anterior (Figura 7)
\[
\begin{gather}
\mathbf E=\underset{\theta_0\rightarrow0}{\lim}-\frac{1}{4\pi\epsilon_0}\;\frac{Q}{a^2}\frac{2}{\theta_0}\operatorname{sen}\frac{\theta_0}{2}\;\mathbf j
\end{gather}
\]
invirtiendo el término
\( \frac{2}{\theta_0} \)
y pasándolo al denominador
\[
\begin{gather}
\mathbf E=\underset{\theta_0\rightarrow 0}{\lim}-{\frac{1}{4\pi\epsilon_0}\frac{Q}{a^2}\dfrac{\operatorname{sen}\dfrac{\theta_0}{2}}{\dfrac{\theta_0}{2}}\;\mathbf j}
\end{gather}
\]
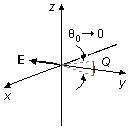
Usando el limite
\( \underset{x\rightarrow 0}{\lim}{\dfrac{\operatorname{sen}x}{x}}=1 \)
\[
\begin{gather}
\mathbf E=-{\frac{1}{4\pi\epsilon_0}}\frac{Q}{a^2}\underbrace{\;\underset{\theta_0\rightarrow 0}{\lim }{\dfrac{\operatorname{sen}\dfrac{\theta_0}{2}}{\dfrac{\theta_0}{2}}}}_{1}\;\mathbf j
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=-{\frac{Q}{4\pi\epsilon_0a^2}}\;\mathbf j}
\end{gather}
\]
el resultado se reduce al vector campo eléctrico de una carga puntual.
publicidad
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .