Ejercicio Resuelto sobre
publicidad
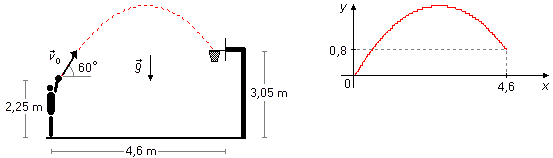
Un jugador de baloncesto lanza el balón hacia la canasta desde una distancia de 4,6 m, formando un ángulo de 60° con la horizontal. La canasta está a una altura de 3,05 m y el balón está a 2,25 m del suelo cuando sale de las manos del jugador. Calcula la velocidad inicial del balón y el tiempo que tarda el balón en ir desde las manos del jugador hasta la canasta.
Datos del problema:
- Distancia del jugador a la canasta: D = 4,6 m;
- Altura del balón al suelo: h = 2,25 m;
- Altura de la canasta al suelo: H = 3,05 m;
- Ángulo de lanzamiento del balón: θ = 60°;
- Aceleración de la gravedad: g =9,8 m/s2.
Tomamos un sistema de referencia en el punto de donde se lanza la pelota, con el eje Ox apuntando hacia la derecha y Oy hacia arriba, la aceleración de la gravedad está apuntando hacia abajo. La pelota es lanzada desde el origen del sistema de referencia, (x0, y0) = (0, 0). La coordenada y1 del punto donde está la canasta es la diferencia entre la altura de la canasta y la altura de las manos del jugador, y1 = H−h = 3,05−2,25 = 0,8.
Solución
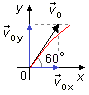
La velocidad inicial v0 puede descomponerse en las direcciones x e y
\[
\begin{gather}
v_{0x}=v_0\cos 60°\\[10pt]
v_{0y}=v_0\operatorname{sen}60°
\end{gather}
\]
De la Trigonometría,
\( \cos 60°=\dfrac{1}{2} \)
y
\( \operatorname{sen}60°=\dfrac{\sqrt{3\;}}{2} \)
\[
\begin{gather}
v_{0x}=\frac{1}{2}v_0 \tag{I}
\end{gather}
\]
\[
\begin{gather}
v_{0y}=\frac{\sqrt{3\;}}{2}v_0 \tag{II}
\end{gather}
\]
En la dirección x no hay aceleración actuando sobre la pelota, está en
Movimiento Rectilíneo Uniforme (MRU) dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_x=S_{0x}+v_xt}
\end{gather}
\]
como en el movimiento uniforme vx = v0x es constante, podemos
sustituir vx por el valor de (I) y S0x = 0
\[
\begin{gather}
S_x=0+\frac{1}{2}v_0t\\[5pt]
S_x=\frac{1}{2}v_0t \tag{III}
\end{gather}
\]
En la dirección y, la pelota está bajo la acción de la aceleración de la gravedad, está en caída
libre, lo cual se expresa como
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S_y=S_{0y}+v_{0y}t-\frac{g}{2}t^2}
\end{gather}
\]
con −g constante (el signo negativo indica que la aceleración de la gravedad está en la
direción opuesta de la orientación del referencia), sustituyendo v0y por el valor
dado por la expresión (II) y S0y = 0
\[
\begin{gather}
S_y=0+\frac{\sqrt{3\;}}{2}v_0t-\frac{9,8}{2}t^2\\[5pt]
S_y=\frac{\sqrt{3\;}}{2}v_0t-4,9t^2 \tag{IV}
\end{gather}
\]
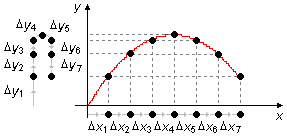
Según la Figura 3, observamos que en el movimiento a lo largo de la dirección x, para intervalos
de tiempo iguales tenemos intervalos de desplazamiento iguales
(Δx1 = Δx2 =
Δx3 = Δx4 = Δx5 =
Δx6 = Δx7). En la dirección y, durante la
ascensión, para intervalos de tiempo iguales tenemos intervalos de desplazamiento más pequeños, la
pelota está siendo frenada por la acción de la gravedad
(Δy1 > Δy2 > Δy3 >
Δy4) hasta que la velocidad vy se vuelve igual a cero. Luego,
la acción de la gravedad comienza a tirar la pelota de vuelta hacia la canasta con velocidad acelerada,
por lo tanto, para intervalos de tiempo iguales tenemos desplazamientos cada vez mayores
(Δy5 < Δy6 < Δy7).
Sustituyendo la distancia del jugador a la canasta, Sx = D = 4,6 m, en la ecuación (III)
\[
\begin{gather}
4,6=\frac{1}{2}v_0t \tag{V}
\end{gather}
\]
Sustituyendo la altura de la canasta, altura final, Sx = H−h = 0,8 m,
en la ecuación (IV)
\[
\begin{gather}
0,8=\frac{\sqrt{3\;}}{2}v_0\;t-4,9\;t^2 \tag{VI}
\end{gather}
\]
Las ecuaciones (V) y (VI) forman un sistema de dos ecuaciones con dos incógnitas (v0 y
t)
\[
\begin{gather}
\left\{
\begin{array}{l}
\dfrac{1}{2}v_0t=4,6\\
-4,9t^2+\dfrac{\sqrt{3\;}}{2}v_0t=0,8
\end{array}
\right.
\end{gather}
\]
aislamos el valor de v0 en la primera ecuación del sistema
\[
\begin{gather}
v_0=\frac{2\times 4,6}{t} \tag{VII}
\end{gather}
\]
y sustituimos la ecuación (VII) en la segunda ecuación del sistema
\[
\begin{gather}
-4,9t^2+\frac{\sqrt{3\;}}{\cancel 2}\times\frac{\cancel 2\times4,6}{\cancel{t}}\cancel{t}=0,8\\[5pt]
4,9t^2=1,7\times 4,6-0,8\\[5pt]
t^2=\frac{7}{4,9}\\[5pt]
t^2=1,4\\[5pt]
t=\sqrt{1,4\;}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{t\approx 1,2\;\mathrm s}
\end{gather}
\]
sustituyendo este valor en la ecuación (VII)
\[
\begin{gather}
v_0=\frac{2\times 4,6}{1,2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_0\approx 7,7\;\mathrm{m/s}}
\end{gather}
\]
publicidad

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .