Ejercicio Resuelto sobre Dinámica
publicidad   



Un bloque, con una masa de 5 kg, es lanzado con una velocidad inicial de 20 m/s en dirección ascendente sobre un plano inclinado de 45°. No hay fricción entre el bloque y el plano inclinado. Determine la distancia que recorrerá el bloque hasta detenerse.


Datos del problema:
  • Masa del bloque:    m = 5 kg;
  • Velocidad inicial del bloque:    v0 = 20 m/s;
  • Ángulo de inclinación del plano:    θ = 45°;
  • Aceleración de la gravedad:    g = 9,8 m/s2;
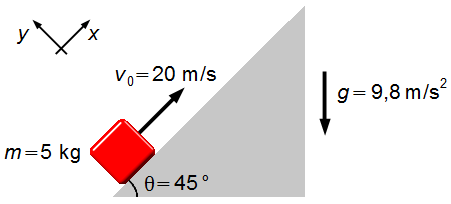
Esquema del problema:

Tomando un sistema de referencia orientado en dirección ascendente del plano inclinado y con el eje-x paralelo al plano (Figura 1).

Figura 1

Haciendo un Diagrama de Cuerpo Libre tenemos las fuerzas que actúan sobre el bloque (Figura 2-A).

  • \( \vec P \): peso del cuerpo;
  • \( \vec N \): fuerza de reacción normal de la superficie sobre el cuerpo.
El peso puede descomponerse en dos, una componente paralela al eje-x, \( {\vec P}_{\small P} \), y la otra normal o perpendicular, \( {\vec P}_{\small N} \) (Figura 2-A).
Dibujamos las fuerzas en un sistema de ejes xy (Figura 2-B).
Figura 2

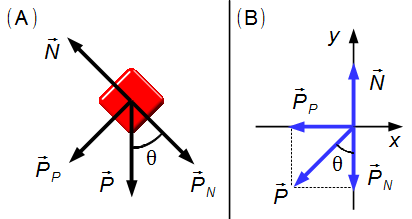
Solución

Aplicando la Segunda Ley de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Dirección x:
\[ \begin{gather} -P_{\small P}=ma \tag{I} \end{gather} \]
la componente paralela del peso es dada por
\[ \begin{gather} P_{\small P}=P\operatorname{sen}\theta \tag{II} \end{gather} \]
el peso es dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{III} \end{gather} \]
sustituyendo la ecuación (III) en la ecuación (II)
\[ \begin{gather} P_{\small P}=mg\operatorname{sen}\theta \tag{IV} \end{gather} \]
sustituyendo la ecuación (IV) en la ecuación (I)
\[ \begin{gather} -\cancel{m}g\operatorname{sen}\theta=\cancel{m}a\\[5pt] a=-g\operatorname{sen}45° \end{gather} \]

Por trigonometría tenemos que   \( \operatorname{sen}45°=\dfrac{\sqrt{2}}{2} \)

\[ \begin{gather} a=-9.8\times\frac{\sqrt{2\;}}{2}\\[5pt] a\approx -6.9\;\mathrm{m/s^2} \end{gather} \]
el signo negativo de la aceleración indica que esta está en sentido contrario a la orientación de la trayectoria y el bloque está siendo frenado.
Aplicando la ecuación de la velocidad en función del desplazamiento
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
El bloque va desacelerando hasta que su velocidad final sea nula, v = 0, y sustituyendo la velocidad inicial dada en el problema y la aceleración calculada anteriormente
\[ \begin{gather} \Delta S=\frac{v^2-v_0^2}{2a}\\[5pt] \Delta S=\frac{0^2-(20)^2}{2\times(-6,9)} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta S\approx 28,0\;\mathrm m} \end{gather} \]
publicidad   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .