Solved Problem on Contours

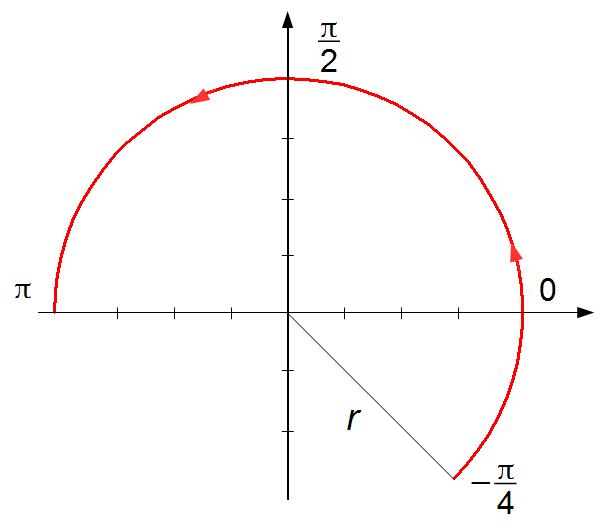
\( \mathsf{b)}\;\; \displaystyle z=r(\cos t+i\operatorname{sen}t)\qquad ,\qquad -\frac{\pi }{4}\leqslant t\leqslant \pi \qquad ,\qquad r\gt 0 \)

The function z is a parametric function of the type

\[ \bbox[#99CCFF,10px] {z(t)=x(t)+iy(t)} \]

Identifying the functions x(t) and y(t)

\[ \begin{align} & x(t)=r\cos t \tag{I}\\[10pt] & y(t)=r\operatorname{sen}t \tag{II} \end{align} \]

squaring the expressions (I) and (II) and adding the two expressions

\[ \begin{gather} \frac{ \begin{matrix} x^{2}=r^{2}\cos^{2}t\\ y^{2}=r^{2}\operatorname{sen}^{2}t \end{matrix} } {x^{2}+y^{2}=r^{2}\cos^{2}t+r^{2}\operatorname{sen}^{2}t}\\[5pt] x^{2}+y^{2}=r^{2}\underbrace{\left(\cos^{2}t+\operatorname{sen}^{2}t\right)}_{1}\\[5pt] x^{2}+y^{2}=r^{2} \tag{III} \end{gather} \]

Graph 1

The function z(t) represents a circunference, for the given interval we have an arc of cinrcunference oriented from \( -{\frac{\pi}{4}} \) to π, (Graph 1).

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .