Solved Problem on Contour Integration

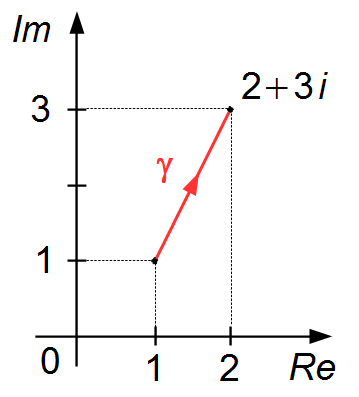
h) \( z=x^{2}y+3xyi \), along the path from the point 1+i to point 2+3i.

Parameterization of the γ curve (Figure 1)

The parameterization of a line is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {z(t)=z_{1}+t(z_{2}-z_{1})} \end{gather} \]

where z₁ and z₂ are the start and end points of the curve, \( z_{1}=1+i \) and \( z_{2}=2+3 i \)

\[ \begin{gather} z(t)=(1+i)+t[(2+3i)-(1+i)]\\[5pt] z(t)=(1+i)+t(2+3i-1-i)\\[5pt] z(t)=(1+i)+t(1+2i)\\[5pt] z(t)=1+i+t+2ti\\[5pt] \qquad \qquad \qquad \qquad \quad z(t)=(1+t)+i(1+2t)\qquad ,\qquad 0\leqslant t\leqslant 1 \tag{I} \end{gather} \]

Figure 1

Derivative of z(t) = (1+t)+i(1+2t)

\[ \begin{gather} z'(t)=\frac{dz}{dt}=1+2i \tag{II} \end{gather} \]

The contour integral is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\int f(z)\;dz=\int f(z(t))z'(t)\;dt} \tag{III} \end{gather} \]

Integration of f(z) = x²y+3xyi

\[ \begin{gather} z=x^{2}y+3xyi \tag{IV} \end{gather} \]

using expression (I) we have f(z(t))

\[ \begin{gather} z(t)=\underbrace{(1+t)}_{x(t)}+\underbrace{(1+2t)}_{y(t)}\;i \tag{V} \end{gather} \]

substituting the values of x(t) and y(t) of expression (V) into expression (IV)

\[ \begin{gather} f(z(t))=(1+t)^{2}(1+2t)+3(1+t)(1+2t)i\\[5pt] f(z(t))=\left(1+2t+t^{2}\right)(1+2t)+3\left(1+2t+t+2t^{2}\right)i\\[5pt] f(z(t))=\left(1+2t+2t+4t^{2}+t^{2}+2t^{3}\right)+3\left(1+3t+2t^{2}\right)i\\[5pt] f(z(t))=\left(1+4t+5t^{2}+2t^{3}\right)+\left(3+9t+6t^{2}\right)i \tag{VI} \end{gather} \]

substituting expressions (II) and (VI) into expression (III)

\[ \begin{split} \int f(z)\;dz &=\int_{0}^{1}\left[\left(1+4t+5t^{2}+2t^{3}\right)+\left(3+9t+6t^{2}\right)i\right](1+2i)\;dt=\\[5pt] &=\int_{0}^{1}\left[\left(1+4t+5t^{2}+2t^{3}\right)(1+2i)+\right.\\ &\qquad \quad\left.+\left(3+9t+6t^{2}\right)(1+2i)i\right]\;dt=\\[5pt] &=\int_{0}^{1}1+4t+5t^{2}+2t^{3}+2i+8ti+10t^{2}i+4t^{3}i+\\ &\qquad \quad+\left(3+9t+6t^{2}\right)(i+2i^{2})\;dt=\\[5pt] &=\int_{0}^{1}1+4t+5t^{2}+2t^{3}+2i+8ti+10t^{2}i+4t^{3}i+\\ &\qquad \quad+\left(3+9t+6t^{2}\right)(i+2.(-1))\;dt=\\[5pt] &=\int_{0}^{1}\left[1+4t+5t^{2}+2t^{3}+2i+8ti+10t^{2}i+4t^{3}i+\right.\\ &\qquad \quad\left.+\left(3+9t+6t^{2}\right)(i-2)\right]\;dt=\\[5pt] &=\int_{0}^{1}\left[1+4t+5t^{2}+2t^{3}+2i+8ti+10t^{2}i+4t^{3}i+\right.\\ &\qquad \quad\left.+3i-6+9ti-18t+6t^{2}i-12t^{2}\right]\;dt=\\[5pt] &=\int_{0}^{1}\left[-5-14t-7t^{2}+2t^{3}+5i+\right.\\ &\qquad \quad\left.+17ti+16t^{2}i+4t^{3}i\right]\;dt=\\[5pt] &=-5\int_{0}^{1}\;dt-14\int_{0}^{1}t\;dt-7\int_{0}^{1}t^{2}\;dt+2\int_{0}^{1}t^{3}\;dt+\\ &\qquad \quad+5i\int_{0}^{1}\;dt+17i\int_{0}^{1}t\;dt+16i\int_{0}^{1}t^{2}\;dt+4i\int_{0}^{1}t^{3}\;dt=\\[5pt] &=-5\;\left(\left.t\right|_{0}^{1}\right)-14\;\left(\left.\frac{t^{2}}{2}\right|_{0}^{1}\right)-7\;\left(\left.\frac{t^{3}}{3}\right|_{0}^{1}\right)+2\;\left(\left.\frac{t^{4}}{4}\right|_{0}^{1}\right)+5i\;\left(\left.t\right|_{0}^{1}\right)+\\ &\qquad \quad+17i\;\left(\left.\frac{t^{2}}{2}\right|_{0}^{1}\right)+16i\;\left(\left.\frac{t^{3}}{3}\right|_{0}^{1}\right)+4i\;\left(\left.\frac{t^{4}}{4}\right|_{0}^{1}\right)=\\[5pt] &=-5-\frac{14}{2}-\frac{7}{3}+\frac{2}{4}+5i+\frac{17}{2}i+\frac{16}{3}i+\frac{4}{4}i=\\[5pt] &=\frac{-60-84-28+6+60i+102i+64i+12i}{12}=\\[5pt] &=\frac{-166+238i}{12}=\frac{-83+119i}{6} \end{split} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\int_{1+i}^{2+3i}f(z)\;dz=\frac{-83+119i}{6}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .