Solved Problem on Contour Integration

f) \( f(z)=y-x^{2} \), along the path formed by two segments, the first segment going from the origin to the point (0, 1), and the second segment going from the point (0, 1) to the point (2, 1).

The curve is formed by two segments γ₁ and γ₂, which must be parameterized separately.
The parameterization of a line is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {z(t)=z_{1}+t(z_{2}-z_{1})} \end{gather} \]

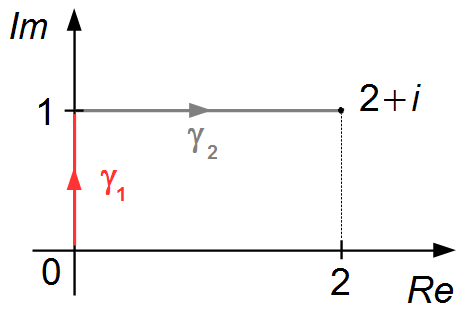
Parameterization of the γ₁ curve (Figure 1)

Start and end points of the curve, \( z_{1}=0+0i \) and \( z_{2}=0+i \)

\[ \begin{gather} z_{\gamma_{1}}(t)=(0+0i)+t[(0+i)-(0+0i)]\\[5pt] \qquad \qquad \qquad \qquad z_{\gamma _{1}}(t)=it\qquad ,\qquad \ 0\leqslant t\leqslant 1 \tag{I} \end{gather} \]

Figure 1

Derivative of z_γ1(t) = it

\[ \begin{gather} z'_{\gamma 1}(t)=\frac{dz_{\gamma 1}}{dt}=i \tag{II} \end{gather} \]

The contour integral is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\int f(z)\;dz=\int f(z(t))z'(t)\;dt} \end{gather} \]

Integration of f(z)=y−x²

\[ \begin{gather} f(z)=y-x^{2} \tag{III} \end{gather} \]

Integration over the γ₁ curve

\[ \begin{gather} I_{1}=\int_{\gamma 1}f(z_{\gamma 1}(t))z'_{\gamma 1}(t)\;dt \tag{IV} \end{gather} \]

using expression (I) we have f(z_γ1(t))

\[ \begin{gather} z_{\gamma 1}(t)=\underbrace{\ 0\ }_{x(t)}+\underbrace{\ t\ }_{y(t)}i \tag{V} \end{gather} \]

substituting the values of x(t) and y(t) of expression (V) into expression (III)

\[ \begin{gather} f(z_{\gamma 1}(t))=t-0^{2}\\ f(z_{\gamma1}(t))=t \tag{VI} \end{gather} \]

substituting expressions (II) and (VI) into expression (IV)

\[ \begin{align} I_{1} &=\int_{0}^{1}(t)(i)\;dt=\int_{0}^{1}ti\;dt=\\[5pt] &=i\int_{0}^{1}t\;dt=i\;\left(\left.\frac{t^{2}}{2}\;\right|_{0}^{1}\right)=\\[5pt] &=i\left(\frac{1}{2}\right)=\frac{1}{2}i \tag{VII} \end{align} \]

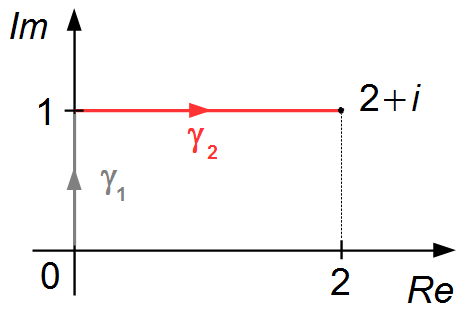
Parameterization of the γ₂ curve (Figure 2)

Start and end points of the curve, \( z_{2}=0+i \) and \( z_{3}=2+i \)

\[ \begin{gather} z_{\gamma_{2}}(t)=(0+i)+t[(2+1i)-(0+i)]\\[5pt] z_{\gamma_{2}}(t)=i+t[2+i-i]\\[5pt] \qquad \qquad \qquad \qquad z_{\gamma_{2}}(t)=2t+i\qquad ,\qquad 0\leqslant t\leqslant 1 \tag{VIII} \end{gather} \]

Figure 2

Derivative of z_γ2(t) = 2t+i

\[ \begin{gather} z'_{\gamma 2}(t)=\frac{dz}{dt}=2 \tag{IX} \end{gather} \]

Integration of f(z)=y−x²

Integration over the γ₂ curve

\[ \begin{gather} I_{2}=\int_{\gamma 2}f(z_{\gamma 2}(t))z'_{\gamma 2}(t)\;dt \tag{X} \end{gather} \]

using expression (VIII) we have f(z_γ2(t))

\[ \begin{gather} z_{\gamma 2}(t)=\underbrace{\ 2t\ }_{x(t)}+\underbrace{\ 1\ }_{y(t)}i \tag{XI} \end{gather} \]

substituting the values of x(t) and y(t) from expression (XI) into expression (III)

\[ \begin{gather} f(z_{\gamma 2}(t))=1-(2t)^{2}\\ f(z_{\gamma 2}(t))=1-4t^{2} \tag{XII} \end{gather} \]

substituting expressions (IX) and (XII) into expression (X)

\[ \begin{align} I_{2} &=\int_{0}^{1}(1-4t^{2})\times(2)\;dt=\int_{0}^{1}(2-8t^{2})\;dt= \\[5pt] &=2\int_{0}^{1}\;dt-8\int_{0}^{1}t^{2}\;dt=2\;\left(\left.t\;\right|_{0}^{1}\right)-8\;\left(\left.\frac{t^{3}}{3}\;\right|_{0}^{1}\right)=\\[5pt] &=2\times(1)-8\times\left(\frac{1}{3}\right)=2-\frac{8}{3}=\frac{6-8}{3}=-{\frac{2}{3}} \tag{XIII} \end{align} \]

The final result will be given by the sum of the integrals over the two segments (VII) and (XIII)

\[ \begin{gather} I=I_{1}+I_{2}\\[5pt] I=\frac{1}{2}i-\frac{2}{3}\\[5pt] I=\frac{3i-4}{6} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\int_{0}^{2+i}f(z)\;dz=\frac{-4+3i}{6}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .