Solved Problem on Cauchy's Integral Formula
advertisement
b) \( \displaystyle \oint_{{C}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz \)

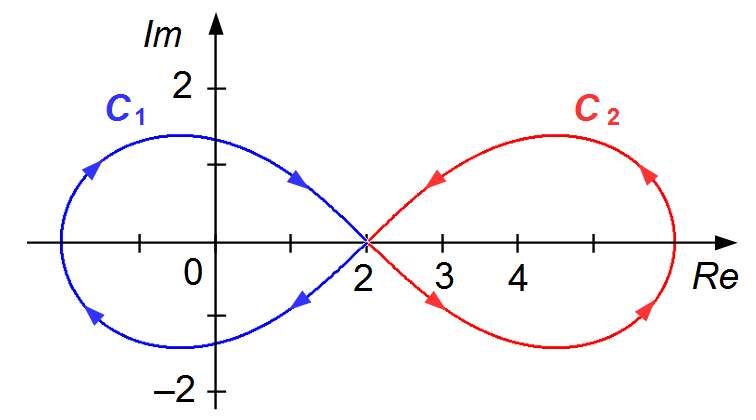
The path is given by contour C (Figure 1). We can divide contour C into two parts, a
contour C1 traversed clockwise on the right side, the integration will be negative. And
a contour C2 traversed counterclockwise on the left side, the integration will be
positive. Only the point z = 0 is inside the region determined by contour C1,
and only the point
\( z-3=0\Rightarrow z=3 \)
is inside the region determined by contour C2.
\[
\begin{gather}
\oint_{{C}}\frac{z}{(z+1)(z-2)}\;dz=\underbrace{-{\oint_{{C_{1}}}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz}_{I_{1}}+\underbrace{\oint_{{C_{2}}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz}_{I_{2}}
\end{gather}
\]
The integral will be given by the sum of the integrals I1 and I2.The Cauchy Integral Formula in the general form is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f^{(n)}(z_{0})=\frac{{n}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz} \tag{I}
\end{gather}
\]
Identifying the terms of the integrals.
- Integral I1:
\[
\begin{gather}
\frac{{
\bbox[#FFCC66,2px]
{n}
}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{
\bbox[#FFFF66,2px]
{f(z)}
}{\left(z-
\bbox[#FFD9CC,2px]
{z_{0}}
\right)^{
\bbox[#FFCC66,2px]
{n}
+1}}\;dz=-\oint_{C}
\bbox[#FFFF66,2px]
{\frac{\operatorname{e}^{z}}{(z-3)}}
\frac{1}{\left[z-
\bbox[#FFD9CC,2px]
{0}
\right]^{
\bbox[#FFCC66,2px]
{0}
+1}}\;dz
\end{gather}
\]
we have
\( f(z)=\frac{\operatorname{e}^{z}}{(z-3)} \),
z0 = 0 and n = 0, writing the expression (I) for the integral
\[
\begin{gather}
I_{1}=\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\frac{2\pi\mathrm{i}}{n!}\;f^{(n)}(z_{0})\\[5pt]
I_{1}=-{\oint_{{C_{1}}}}\frac{\operatorname{e}^{z}}{z(z-3)}=\frac{2\pi\mathrm{i}}{0!}\;f^{(0)}(0)\\[5pt]
I_{1}=2\pi\mathrm{i}\;\times\left[\frac{\operatorname{e}^{0}}{0-3}\right]\\[5pt]
I_{1}=-{\frac{2\pi\mathrm{i}}{3}} \tag{II}
\end{gather}
\]
- Integral I2:
\[
\begin{gather}
\frac{{
\bbox[#FFCC66,2px]
{n}
}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{
\bbox[#FFFF66,2px]
{f(z)}
}{\left(z-
\bbox[#FFD9CC,2px]
{z_{0}}
\right)^{
\bbox[#FFCC66,2px]
{n}
+1}}\;dz=-\oint_{C}
\bbox[#FFFF66,2px]
{\frac{\operatorname{e}^{z}}{z}}
\frac{1}{\left[z-
\bbox[#FFD9CC,2px]
{3}
\right]^{
\bbox[#FFCC66,2px]
{0}
+1}}\;dz
\end{gather}
\]
we have
\( f(z)=\frac{\operatorname{e}^{z}}{z} \),
z0 = 3 and n = 0, writing the expression (I) for the integral
\[
\begin{gather}
I_{2}=\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\frac{2\pi\mathrm{i}}{n!}\;f^{(n)}(z_{0})\\[5pt]
I_{2}=\oint_{{C_{2}}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz=\frac{2\pi\mathrm{i}}{0!}\;f^{(0)}(3)\\[5pt]
I_{2}=2\pi\mathrm{i}\;\times\left(\frac{\operatorname{e}^{3}}{3}\right)\\[5pt]
I_{2}=\frac{2\operatorname{e}^{3}\pi\mathrm{i}}{3} \tag{III}
\end{gather}
\]
The result of the integral will be given by the difference in the values of (II) and (III)
\[
\begin{gather}
\oint_{{C}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz=I_{1}-I_{2}\\[5pt]
\oint_{{C}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz=-{\frac{2\pi\mathrm{i}}{3}}-\frac{2\operatorname{e}^{3}\pi \mathrm{i}}{3}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\oint_{{C}}\frac{\operatorname{e}^{z}}{z(z-3)}\;dz=-\frac{2\pi\mathrm{i}}{3}\left(\operatorname{e}^{3}+1\right)}
\end{gather}
\]
Note 1: We do not need to know the equation that describes the contour C for the
calculation, it is enough to know if the singularity points are inside or outside the region determined
by the contour.
Note 2: f(0) represents the calculation of the function at the point z0 without derivative.
Note 2: f(0) represents the calculation of the function at the point z0 without derivative.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .