Solved Problem on Cauchy's Integral Formula
advertisement
h) \( \displaystyle \oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz \)
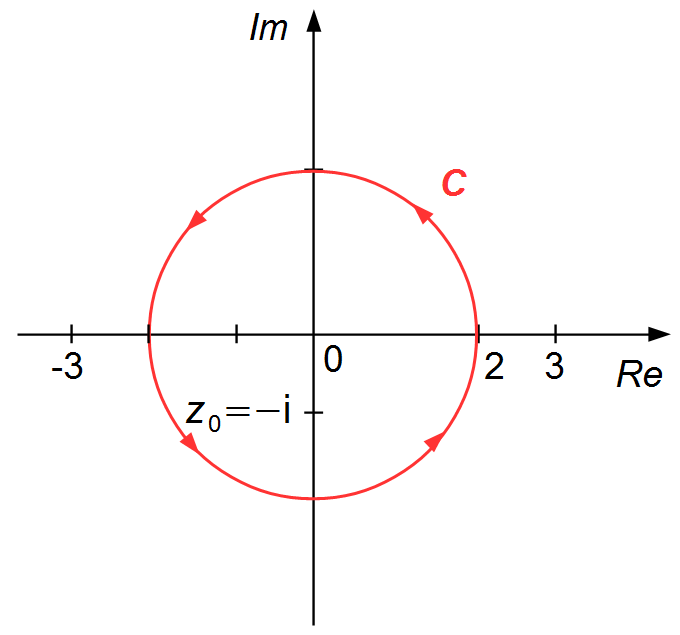
The path of integration is given by the circle of radius 2, centered at the origin (0, 0), traversed
counterclockwise (Figure 1).
The general form of Cauchy's Integral Formula given by
The general form of Cauchy's Integral Formula given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f^{(n)}(z_{0})=\frac{{n}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz} \tag{I}
\end{gather}
\]
Identifying the terms of the integral
\[
\begin{gather}
\frac{n!}{2\pi \mathrm{i}}\;\oint_{C}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\oint_{|z|=2}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz
\end{gather}
\]
the points
\( z^{2}-9=0\Rightarrow z^{2}=9\Rightarrow z=\pm 3 \)
are outside the region determined by de close contur C, only the point
\( z+\mathrm{i}=0\Rightarrow z=-\mathrm{i} \)
that is inside the region will be used in the calculation of the integral
\[
\begin{gather}
\frac{{
\bbox[#FFCC66,2px]
{n}
}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{
\bbox[#FFFF66,2px]
{f(z)}
}{\left(z-
\bbox[#FFD9CC,2px]
{z_{0}}
\right)^{
\bbox[#FFCC66,2px]
{n}
+1}}\;dz=\oint_{{|z|=2}}
\bbox[#FFFF66,2px]
{\frac{z}{\left(z^{2}-9\right)}}
\frac{1}{\left[z-(
\bbox[#FFD9CC,2px]
{-\mathrm{i}}
)\right]^{
\bbox[#FFCC66,2px]
{0}
+1}}\;dz
\end{gather}
\]
we have
\( f(z)=\frac{z}{\left(z^{2}-9\right)} \),
z0 = −i and n = 0, writing the expression (I) for the given integral
\[
\begin{gather}
\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\frac{2\pi\mathrm{i}}{n!}\;f^{(n)}(z_{0})\\[5pt]
\oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz=\frac{2\pi\mathrm{i}}{0!}\;f^{(0)}(-\mathrm{i})\\[5pt]
\oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz=2\pi\mathrm{i}\;\frac{(-\mathrm{i})}{\left[(-\mathrm{i})^{2}-9\right]}\\[5pt]
\oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz=2\pi\mathrm{i}^{2}\;\frac{1}{\left[\mathrm{i}^{2}-9\right]}\\[5pt]
\oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz=2\pi\times(-1)\;\times\frac{1}{\left[-1-9\right]}\\[5pt]
\oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz=-\cancel{2}\pi\;\frac{1}{-\cancelto{5}{10}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\oint_{{|z|=2}}\frac{z}{\left(z^{2}-9\right)(z+\mathrm{i})}\;dz=\frac{\pi}{5}}
\end{gather}
\]
Note 1: The path traversed
\( |\;z\;|=2 \)
is a circle. For a complex number
\( z=x+\mathrm{i}y \),
the absolute value is given by
\( \sqrt{x^{2}+y^{2}\;}=2 \),
squaring both sides of equation
\( \left(\sqrt{x^{2}+y^{2}\;}\right)^{2}=2^{2} \),
we obtain the equation of a circle
\( (x-0)^{2}+(y-0)^{2}=2^{2}, \)
Note 2: f(0) represents the calculation of the function at the point z0 without derivative.
\[ (x-0)^{2}+(y-0)^{2}=2^{2} \]
with a radius equal to 2 and center at the origin (0, 0).
Note 2: f(0) represents the calculation of the function at the point z0 without derivative.
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .