Solved Problem on Coulomb's Law and Electric Field
advertisement
Determine the electric field vector of a dipole at the points along the straight line joining the two charges on the dipole. Check the solution for the points far away from the center of the dipole.
Problem diagram:
The vector r locates the point P, where we want to calculate the electric field relative to the origin, and is written as \( \mathbf{r}=x\;\mathbf{i} \). The vector r1 is the distance from the origin to the charge −q, it is given by \( \mathbf{r}_{1}=-d\;\mathbf{i} \). The vector r−r1 is the distance from de charge to the point P, is given by \( \mathbf{r}-\mathbf{r}_{1}=x\;\mathbf{i}-(-d\;\mathbf{i})=(x+d)\;\mathbf{i} \), (Figure 1).
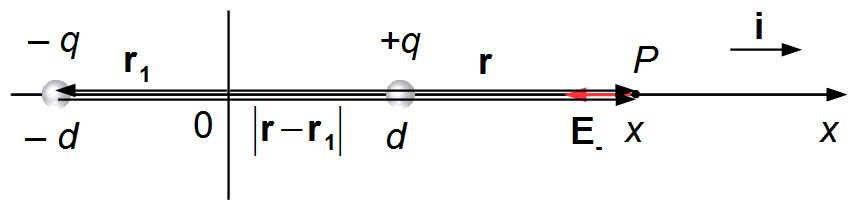
The vector r is the same as in the previous situation. The vector r2 is the distance from the origin to the charge +q and is given by \( \mathbf{r}_{2}=d\;\mathbf{i} \). The vector r−r2 is the distance from the charge to the point P and is given by \( \mathbf{r}-\mathbf{r}_{2}=(x-d)\;\mathbf{i} \), (Figure 2).
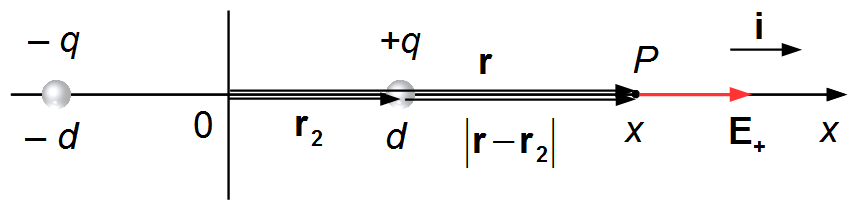
Solution
The electric field vector of a discrete system of charges is calculated by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\;\sum_{i=1}^{n}\;\frac{q_{i}}{\left|\mathbf{r}-\mathbf{r}_{i}\right|^{2}}\;\frac{\mathbf{r}-\mathbf{r}_{i}}{\left|\mathbf{r}-\mathbf{r}_{i}\right|}}
\end{gather}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\left\{\frac{q_{1}}{\left|\mathbf{r}-\mathbf{r}_{1}\right|^{2}}\;\frac{\mathbf{r}-\mathbf{r}_{1}}{\left|\mathbf{r}-\mathbf{r}_{1}\right|}+\frac{q_{2}}{\left|\mathbf{r}-\mathbf{r}_{2}\right|^{2}}\;\frac{\mathbf{r}-\mathbf{r}_{2}}{\left|\mathbf{r}-\mathbf{r}_{2}\right|}\right\}
\end{gather}
\]
The denominators of the above equation are written as
\( \left|\mathbf{r}-\mathbf{r}_{1}\right|=\sqrt{(x+d)^{2}\;}=x+d \),
\( \left|\mathbf{r}-\mathbf{r}_{1}\right|^{2}=(x+d)^{2} \),
\( \left|\mathbf{r}-\mathbf{r}_{2}\right|=\sqrt{(x-d)^{2}\;}=x-d \)
and
\( \left|\mathbf{r}-\mathbf{r}_{2}\right|^{2}=(x-d)^{2} \).
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\left\{\frac{-q}{\left(x+d\right)^{\cancelto{2}{3}}}\;\cancel{\left(x+d\right)}\;\mathbf{i}+\frac{q}{\left(x-d\right)^{\cancelto{2}{3}}}\;\cancel{\left(x-d\right)}\;\mathbf{i}\right\}\\[5pt]
\mathbf{E}=\frac{q}{4\pi\epsilon_{0}}\left\{\frac{-1}{\left(x+d\right)^{2}}+\frac{1}{\left(x-d\right)^{2}}\right\}\;\mathbf{i}\\[5pt]
\mathbf{E}=\frac{q}{4\pi\epsilon_{0}}\left\{\frac{-\left(x-d\right)^{2}+\left(x+d\right)^{2}}{\left(x+d\right)^{2}\left(x-d\right)^{2}}\right\}\;\mathbf{i}\\{}\\
\mathbf{E}=\frac{q}{4\pi\epsilon_{0}}\left\{\frac{-\left(x^{2}-2xd+d^{2}\right)+x^{2}+2xd+d^{2}}{\left(x+d\right)^{2}\left(x-d\right)^{2}}\right\}\;\mathbf{i}\\[5pt]
\mathbf{\text{E}}=\frac{q}{4\pi\epsilon_{0}}\left\{\frac{-x^{2}+2xd-d^{2}+x^{2}+2xd+d^{2}}{\left(x+d\right)^{2}\left(x-d\right)^{2}}\right\}\;\mathbf{i}\\[5pt]
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\frac{4qxd}{\left(x+d\right)^{2}\left(x-d\right)^{2}}\;\mathbf{i}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{\pi \epsilon_{0}}\frac{qxd}{\left(x+d\right)^{2}\left(x-d\right)^{2}}\;\mathbf{i}}
\end{gather}
\]
Note 1: In a one-dimensional problem, the vector solution is the same as the scalar solution.
Note 2: The dipole moment p is given by the product of the charge and the distance between them, for the result above, we have the magnitude
Note 2: The dipole moment p is given by the product of the charge and the distance between them, for the result above, we have the magnitude
\[
\begin{gather}
p=q\times (2d)
\end{gather}
\]
the solution is written as
\[
\begin{gather}
\mathbf{E}=\frac{1}{2\pi \epsilon_{0}}\frac{px}{\left(x+d\right)^{2}\left(x-d\right)^{2}}\;\mathbf{i}
\end{gather}
\]
For points far from the center of the dipole we have, x≫d, we can neglect the term in d2 in the denominator, and the solution will be
\[
\begin{gather}
\mathbf{E}=\frac{1}{\pi \epsilon_{0}}\frac{q\cancel{x}d}{x^{\cancelto{3}{4}}}\;\mathbf{i}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{\pi \epsilon_{0}}\frac{qd}{x^{3}}\;\mathbf{i}}
\end{gather}
\]
Note: Using the dipole moment the solution is written as
\[
\begin{gather}
\mathbf{E}=\frac{1}{2\pi \epsilon_{0}}\frac{p}{x^{3}}\;\mathbf{i}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .