Solved Problem on One-dimensional Motion

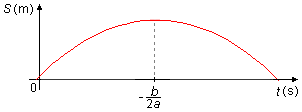
The motion of a particle is described by a Quadratic Function in t, which represents the time given in seconds, as shown in the figure. Determine:
a) The equation of displacement as a function of time;
b) The instant in which the motion reverses the direction;
c) The equation of velocity as a function of time;
d) The graph of velocity versus time.

Solution

a) The standard form of a Quadratic Function is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {S(t)=at^{2}+bt+c} \tag{I} \end{gather} \]

From the graph, we can get 3 points \( (t_{1},S_{1})=(1,28) \), \( (t_{2},S_{2})=(2,42) \) and \( (t_{4},S_{4})=(4,58) \), substituting these points in the expression (I)

\[ \begin{gather} \left\{ \begin{array}{l} 28=a.1^{2}+b.1+c\\ 42=a.2^{2}+b.2+c\\ 58=a.4^{2}+b.4+c \end{array} \right.\\[10pt] \left\{ \begin{array}{l} a+b+c=28\\ 4a+2b+c=42\\ 16a+4b+c=58 \end{array} \right. \tag{II} \end{gather} \]

The three equations can be written as a system (II) of three equations to three unknowns, a, b and c.
Subtracting the first equation of the second equation in the system (II)

\[ \begin{gather} \frac{ \begin{aligned} 4a+2b+c=42\\ (-)\quad a+b+c=28 \end{aligned} } {\qquad 3a+b+0=14}\\ \qquad 3a+b=14 \tag{III} \end{gather} \]

Subtracting the second equation of the third equation in the system(II)

\[ \begin{gather} \frac{ \begin{aligned} 16a+4b+c=58\\ (-)\quad 4a+2b+c=42 \end{aligned} } {\qquad 12a+2b+0=16}\\ \qquad 12a+2b=16 \tag{IV} \end{gather} \]

Expressions (III) and (IV) can be written as a system of two equations to two unknowns, a e b

\[ \left\{ \begin{array}{l} 3a+b=14\\ 12a+2b=16 \end{array} \tag{V} \right. \]

solving the first equation in the system (V) for b, and substituting in the second equation

\[ \begin{gather} b=14-3a \tag{VI} \end{gather} \]

\[ \begin{gather} 12 a+2.(14-3 a)=16\\ 12 a +28-6 a=16\\ 6 a=16-28\\ a=-\frac{12}{6}\\ a=-2 \end{gather} \]

substituting this value in the expression (VI)

\[ \begin{gather} b=14-3.(-2)\\ b=14+6\\ b=20 \end{gather} \]

substituting a and b in the first equation of the system (II)

\[ \begin{gather} -2+20 +c=28\\ c=28-18\\ c=10 \end{gather} \]

substituting a, b, and c in the expression (I), we have the expression for the displacement as a function of time

\[ \bbox[#FFCCCC,10px] {S=10+20-2t^{2}} \]

Note: Comparing with the equation of displacement as a function of time with constant acceleration, \( S=10+20t-2t^{2} \), we see that the initial position is S₀ = 10 m, the initial speed v₀ = 20 m/s and the acceleration \( \frac{a}{2}=-2 \Rightarrow a=-2.2 \Rightarrow a=4 \;\text{m/s}^{2}. \)

\[ \frac{a}{2}=-2 \Rightarrow a=-2.2 \Rightarrow a=4 \;\text{m/s}^{2}. \]

b) The equation describing the motion is a parabola with the negative coefficient a<0, this parabola has concavity downward. Motion is initially in the same direction of reference frame, the positions increases, up to a moment in which it reverses and begins to move in the opposite direction, the positions decreases, this point is the vertex of the parabola (Graph 1) given by

Graph 1

\[ \begin{gather} t=-{\frac{b}{2a}}=-{\frac{v_{0}}{2a}}\\ t=-{\frac{20}{2.(-2)}}\\ t=-{\frac{20}{-4}} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {t=5\;\text{s}} \]

c) Using the data obtained in item (a) for the initial speed, v₀ = 20 m/s, and for acceleration, a = −4 m/s², the equation of the velocity as a function of time will be

\[ \bbox[#FFCCCC,10px] {v=20-4t} \]

d) For the construction of the velocity-time graph, v = f(t), we use the equation of item (c), assigning values to t and obtaining v we have Table 1, and from the table, we construct Graph 2.

t (s)	`\( v=20-4t \)`	v(t) (m/s)
0	`\( v(0)=20-4\times 0 \)`	20
2	`\( v(2)=20-4\times 2 \)`	12
4	`\( v(4)=20-4\times 4 \)`	4
6	`\( v(6)=20-4\times 6 \)`	−4
8	`\( v(8)=20-4\times 8 \)`	−12
10	`\( v(10)=20-4\times 10 \)`	−20

Table 1

Graph 2

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .