Exercício Resolvido de Movimento Unidimensional
publicidade
Um ponto material realiza um movimento descrito por uma Função do 2.° Grau em t, que
representa o tempo dado em segundos, de acordo com a figura. Determine:
a) A equação do movimento;
b) O instante em que o movimento passa de progressivo a retrógrado ou regressivo;
c) A equação da velocidade;
d) O gráfico da velocidade.
a) A equação do movimento;
b) O instante em que o movimento passa de progressivo a retrógrado ou regressivo;
c) A equação da velocidade;
d) O gráfico da velocidade.

Solução
a) A expressão geral para uma Função do 2.º Grau é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S(t)=at^{2}+bt+c} \tag{I}
\end{gather}
\]
A partir do gráfico podemos obter 3 pontos
\( (t_{1},S_{1})=(1,28) \),
\( (t_{2},S_{2})=(2,42) \)
e
\( (t_{4},S_{4})=(4,58) \),
substituindo estes pontos na expressão (I)
\[
\begin{gather}
\left\{
\begin{array}{l}
28=a.1^{2}+b.1+c\\
42=a.2^{2}+b.2+c\\
58=a.4^{2}+b.4+c
\end{array}
\right.\\[10pt]
\left\{
\begin{array}{l}
a+b+c=28\\
4a+2b+c=42\\
16a+4b+c=58
\end{array}
\right. \tag{II}
\end{gather}
\]
as três equações formam o sistema (II) de três equações a três incógnitas, a, b e
c.Subtraindo a primeira equação da segunda equação do sistema (II)
\[
\begin{gather}
\frac{
\begin{aligned}
4a+2b+c=42\\
(-)\quad a+b+c=28
\end{aligned}
}
{\qquad 3a+b+0=14}\\
\qquad 3a+b=14 \tag{III}
\end{gather}
\]
Subtraindo a segunda equação da terceira equação do sistema (II)
\[
\begin{gather}
\frac{
\begin{aligned}
16a+4b+c=58\\
(-)\quad 4a+2b+c=42
\end{aligned}
}
{\qquad 12a+2b+0=16}\\
\qquad 12a+2b=16 \tag{IV}
\end{gather}
\]
As expressões (III) e (IV) formam um sistema de duas equações a duas incógnitas, a e b
\[
\left\{
\begin{array}{l}
3a+b=14\\
12a+2b=16
\end{array} \tag{V}
\right.
\]
isolando o valor de b na primeira equação do sistema (V) e substituindo na segunda equação
\[
\begin{gather}
b=14-3a \tag{VI}
\end{gather}
\]
\[
\begin{gather}
12 a+2.(14-3 a)=16\\
12 a +28-6 a=16\\
6 a=16-28\\
a=-\frac{12}{6}\\
a=-2
\end{gather}
\]
substituindo este valor na expressão (VI)
\[
\begin{gather}
b=14-3.(-2)\\
b=14+6\\
b=20
\end{gather}
\]
substituindo os valores de a e b na primeira equação do sistema (II)
\[
\begin{gather}
-2+20 +c=28\\
c=28-18\\
c=10
\end{gather}
\]
substituindo a, b e c na expressão (I) temos a expressão do movimento
\[ \bbox[#FFCCCC,10px]
{S=10+20-2t^{2}}
\]
Observação: Comparando com a equação do Movimento Retilíneo Uniformemente Variado
(M.R.U.V.),
\( S=10+20t-2t^{2} \),
vemos que o espaço inicial vale S0 = 10 m, a velocidade inicial
v0 = 20 m/s e a aceleração
\( \frac{a}{2}=-2 \Rightarrow a=-2.2 \Rightarrow a=4 \;\text{m/s}^{2}. \)
\[ \frac{a}{2}=-2 \Rightarrow a=-2.2 \Rightarrow a=4 \;\text{m/s}^{2}. \]
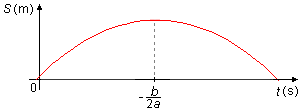
b) A equação que descreve o movimento é uma parábola com o coeficiente a negativo a<0, esta
parábola possui concavidade voltada para baixo (“boca” para baixo). O movimento é inicialmente
progressivo, o espaço aumenta, até um instante em que se inverte e começa a ser retrógrado, o espaço
diminui, este ponto é o vértice da parábola (Gráfico 1) dado por
\[
\begin{gather}
t=-{\frac{b}{2a}}=-{\frac{v_{0}}{2a}}\\
t=-{\frac{20}{2.(-2)}}\\
t=-{\frac{20}{-4}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=5\;\text{s}}
\]
c) Usando os dados obtidos no item (a) para a velocidade inicial, v0 = 20 m/s e para a
aceleração, a = −4 m/s2, a equação horária da velocidade será
\[ \bbox[#FFCCCC,10px]
{v=20-4t}
\]
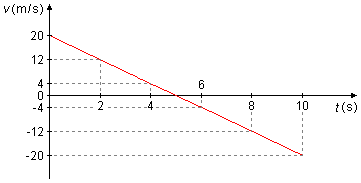
d) Para a construção do gráfico da velocidade em função do tempo, v = f(t) usamos a
equação do item (c) atribuindo valores a t e obtendo v, construímos a Tabela 1 e com os
valores da tabela construímos o Gráfico 2.
| t (s) | \( v=20-4t \) | v(t) (m/s) |
|---|---|---|
| 0 | \( v(0)=20-4.0 \) | 20 |
| 2 | \( v(2)=20-4.2 \) | 12 |
| 4 | \( v(4)=20-4.4 \) | 4 |
| 6 | \( v(6)=20-4.6 \) | −4 |
| 8 | \( v(8)=20-4.8 \) | −12 |
| 10 | \( v(10)=20-4.10 \) | −20 |
Tabela 1
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .