Solved Problem on Dynamics
advertisement
A cart moves over a straight and horizontal surface. In the cart there is an inclined plane, making an
angle θ with the horizontal plane. On the plane is placed a body, the coefficient of friction
between the body and the plane is μ. Determine the acceleration of the cart, so that the body is
about to rise the plane. Assume g for the acceleration due to gravity.

Problem data:
- Angle of the inclined plane: θ;
- Coefficient of friction between the body and the plan: μ;
- Acceleration due to gravity: g.
We choose a frame of reference with the x-axis parallel to the inclined plane and direction
downward.
The ground (Earth), assumed without acceleration, is an inertial referential. The cart has acceleration a relative to the ground, non-inertial referential. For the body to remain at rest on the cart, it must have the same acceleration of the cart relative to the ground (Figure 1).
The ground (Earth), assumed without acceleration, is an inertial referential. The cart has acceleration a relative to the ground, non-inertial referential. For the body to remain at rest on the cart, it must have the same acceleration of the cart relative to the ground (Figure 1).

Solution
Drawing a free-body diagram, we have the forces that act on it (Figure 2).
- \( {\vec F}_{g} \): gravitational force;
- \( \vec{N} \): normal reaction force;
- \( {\vec{F}}_{f} \): force of friction between the plane and block.

As the body is about to rise, we have the force of friction \( {\vec F}_{f} \) between the plane and the body in the downward direction of the plane opposing this movement.
The gravitational \( {\vec F}_{g} \) force can be decomposed into two components, one component parallel to the x-axis, \( {\vec F}_{gx} \), and the other component normal or perpendicular, \( {\vec F}_{gy} \). In the triangle in the right in the Figure 3-A we see that the gravitational force \( {\vec F}_{g} \) is perpendicular to the horizontal plane makes a 90° angle, the angle between the inclined plane and the horizontal plane is equal to θ, as the sum of the interior angles of a triangle equals to 180°, the angle α between the gravitational force and the parallel component should be
\[ \alpha +\theta +90°=180°\Rightarrow \alpha=180°-\theta -90°\Rightarrow \alpha=90°-\theta \]
The components of the gravitational force in the x and y directions are perpendicular to each
other, in the triangle to the right, we have the angle between the gravitational force
\( {\vec F}_{g} \)
and the component of gravitational force in the y direction,
\( {\vec F}_{gy} \),
is
\[ 90°-\alpha \Rightarrow 90°-(90°-\theta)\Rightarrow 90°-90°+\theta \Rightarrow \theta \]
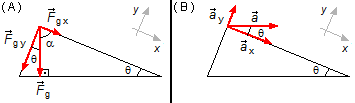
The acceleration of the cart can also be decomposed in the x and y directions (Figure 3-B). The angle between the acceleration \( \vec{a} \) and the component of the acceleration in the direction of the inclined plane \( {\vec a}_{x} \) is θ, the same angle of the inclined plane, are alternate angles.
Drawing the forces in a coordinate system (Figure 4), we can get its components.
The components of the acceleration are given by
The components of the acceleration are given by
\[
\begin{gather}
a_{x}=a\cos \theta \tag{I}
\end{gather}
\]
\[
\begin{gather}
a_{y}=a\sin \theta \tag{II}
\end{gather}
\]
and the gravitational force components are given by
\[
\begin{gather}
F_{gx}=F_{g}\sin \theta \tag{III}
\end{gather}
\]
\[
\begin{gather}
F_{gy}=F_{g}\cos \theta \tag{IV}
\end{gather}
\]

\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{V}
\end{gather}
\]
In the x direction act the friction force and the component of gravitational force in x
direction, applying the expression (I)
\[
\begin{gather}
F_{f}-F_{gx}=ma_{x} \tag{VI}
\end{gather}
\]
substituting the expressions (I) and (III) into expression (VI)
\[
\begin{gather}
F_{f}-F_{g}\sin \theta=ma\cos \theta \tag{VII}
\end{gather}
\]
the force of friction is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{f}=\mu N} \tag{VIII}
\end{gather}
\]
the gravitational force given by is
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{g}=mg} \tag{IX}
\end{gather}
\]
substituting the expressions (VIII) and (IX) into expression (VII)
\[
\begin{gather}
\mu N+mg\sin\theta =ma\cos \theta \\[5pt]
\mu N=ma\cos \theta -mg\sin\theta \tag{X}
\end{gather}
\]
In y direction act the normal force and the component of gravitational force in y direction,
applying the expression (V)
\[
\begin{gather}
N-F_{gy}=ma_{y} \tag{XI}
\end{gather}
\]
substituting expressions (II) and (IV) into expression (XI)
\[
\begin{gather}
N-F_{g}\cos \theta=ma\sin \theta \tag{XII}
\end{gather}
\]
substituting the expression (IX) into expression (XII)
\[
\begin{gather}
N-mg\cos \theta =ma\sin\theta\\[5pt]
N=ma\sin\theta +mg\cos \theta \tag{XIII}
\end{gather}
\]
substituting the expression (XIII) into expression (X)
\[
\begin{gather}
\mu (ma\sin\theta +mg\cos \theta )=ma\cos \theta -mg\sin\theta \\[5pt]
\mu \cancel{m}a\sin\theta +\mu \cancel{m}g\cos \theta =\cancel{m}a\cos\theta -\cancel{m}g\sin\theta\\[5pt]
g\sin \theta +\mu a\sin\theta +\mu g\cos \theta =a\cos \theta\\[5pt]
g\sin \theta +\mu g\cos \theta =a\cos \theta -\mu a\sin \theta\\[5pt]
g(\sin \theta +\mu \cos \theta )=a(\cos \theta -\mu\sin \theta )
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a=g\left(\;\frac{\sin \theta +\mu \cos \theta }{\cos \theta -\mu \sin \theta }\;\right)}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .