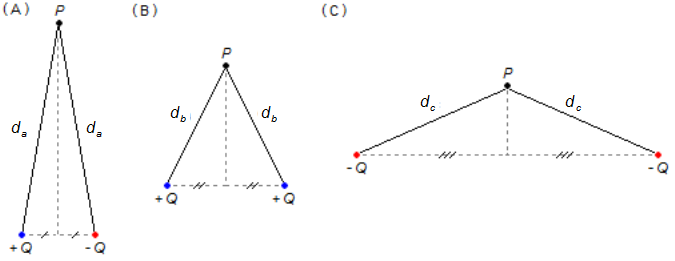
Gelöste Übung zum Elektrischen Potential

Bestimmen Sie das elektrische Potential am Punkt P in den Fällen (A), (B) und (C) der untenstehenden Abbildung, wobei gilt Q = 6 μC, \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) und die Abstände der Ladungen vom Punkt P gegeben sind:
a) d_a = 0,3 m;
b) d_b = 0,1 m;
c) d_c = 0,2 m.

Gegebene Daten:

Betrag der Ladungen: Q=6 μC=6×10⁻⁶ C;
Coulomb-Konstante: \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \) .

Lösung:

Das elektrische Potential an einem Punkt aufgrund mehrerer Ladungen ergibt sich aus der algebraischen Summe der Potentiale jeder einzelnen Ladung

\[ \begin{gather} \bbox[#99CCFF,10px] {V=k_e\frac{Q_1}{d_1}+k_e\frac{Q_2}{d_2}+...+k_e\frac{Q_n}{d_n}} \end{gather} \]

a) Für \( Q_1=+6\times 10^{-6}\;\mathrm C \) , \( Q_2=-6\times 10^{-6}\;\mathrm C \) und \( d_1=d_2=d_a=0,3\;\mathrm m \)

\[ \begin{gather} V=9\times 10^9\times\frac{6\times 10^{-6}}{0,3}+9\times 10^9\times\frac{-6\times 10^{-6}}{0,3} \\[5pt] V=180\times 10^3-180\times 10^3 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {V=0} \end{gather} \]

b) Für \( Q_1=Q_2=+6\times 10^{-6}\;\mathrm C \) und \( d_1=d_2=d_b=0,1\;\mathrm m \)

\[ \begin{gather} V=9\times 10^9\times\frac{6\times 10^{-6}}{0,1}+9\times 10^9\times\frac{6\times 10^{-6}}{0,1} \\[5pt] V=2\times 540\times 10^3 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {V=1,08\times 10^6\;\text V} \end{gather} \]

c) Für \( Q_1=Q_2=-6\times 10^{-6}\;\mathrm C \) und \( d_1=d_2=d_c=0,2\;\mathrm m \)

\[ \begin{gather} V=9\times 10^9\times\frac{\left(-6\times 10^{-6}\right)}{0,2}+9\times 10^9\times\frac{\left(-6\times 10^{-6}\right)}{0,2} \\[5pt] V=\cancel 2\times\left(-\frac{54\times 10^3}{\cancel 2\times 10^{-1}}\right) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {V=-5,4\times 10^5\;\mathrm V} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .