Solved Problem on Kepler's Laws and Gravitation
advertisement
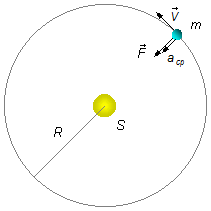
A planet of mass m describes a circular orbit around a star S at a distance R, with a speed such that the duration of each revolution is T. The movement takes place under the action of a force F of constant magnitude, directed towards S. Using acp, K and V to represent the centripetal acceleration, kinetic energy, and velocity of the planet, respectively.
a) Establish the expression of K as a function of F and R, that is K = f(F, R);
b) Establish as a function of R, T and m the expressions of V, acp and K, that is, V = f(R, T, m), acp = f(R, T, m) and K = f(R, T, m);
c) Show that F is given by the expression \( F=A\dfrac{m}{R^{2}} \) where A is a constant;
d) Apply the expressions found by calculating acp, F e K in the case of the Earth around the Sun. Data are: Earth's speed in its orbit 30 km/s, Earth's orbit radius 15×107 km, and Earth's mass 6×1021 t.
Problem data:
- Planet mass: m;
- Distance from planet to star: R;
- Period of the planet's orbit: T;
- Force between planet and star: F;
- Earth's speed in its orbit: vT = 30 km/s;
- Earth orbit radius: RT = 15×107 km;
- Earth Mass: mT = 6×1021 t.
Solution
First, we must convert the Earth's speed, given in kilometers per second (km/s) to meters per second (m/s), the radius of the Earth's orbit given in kilometers (km) to meters (m), and the Earth's mass given in metric tons (t) to kilograms (kg), used in the International System of Units (S.I.).
\[
\begin{gather}
v_{T}=30\;\frac{\cancel{\text{km}}}{\text{s}}\times\frac{1000\;\text{m}}{\cancel{\text{km}}}=30000\;\frac{\text{m}}{\text{s}}=3\times10^{4}\text{m/s}\\[10pt]
R_{T}=15\times10^{7}\;\cancel{\text{km}}\times\frac{1000\;\text{m}}{\cancel{\text{km}}}=15\times10^{7}\times10^{3}\;\text{m}=15\times10^{10}\;\text{m}\\[10pt]
m_{T}=6\times10^{21}\;\cancel{\text{t}}\times\frac{1000\;\text{kg}}{\cancel{\text{t}}}=6\times10^{21}\times10^{3}\;\text{kg}=6\times10^{24}\;\text{t}
\end{gather}
\]
a) The kinetic energy is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{K=\frac{mv^{2}}{2}}
\end{gather}
\]
setting v = V
\[
\begin{gather}
K=\frac{mV^{2}}{2} \tag{I}
\end{gather}
\]
As the planet is revolving around the star, it is subject to a centripetal acceleration given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_{cp}=\frac{v^{2}}{r}} \tag{II}
\end{gather}
\]
setting v = V and r = R in expression (II), the speed will be
\[
\begin{gather}
V^{2}=a_{cp}R \tag{III}
\end{gather}
\]
substituting expression (III) into expression (I)
\[
\begin{gather}
K=\frac{ma_{cp}R}{2} \tag{IV}
\end{gather}
\]
The centripetal force is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{cp}=ma_{cp}}
\end{gather}
\]
setting the centripetal force equal to the force between the star and the planet, given in the problem,
Fcp = F
\[
\begin{gather}
F=ma_{cp} \tag{V}
\end{gather}
\]
substituting expression (V) into expression (IV)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{K(F,R)=\frac{FR}{2}}
\end{gather}
\]
b) The velocity of a body with constant speed is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r}
\end{gather}
\]
\[
\begin{gather}
V=\omega R \tag{VI}
\end{gather}
\]
the angular speed ω is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega =\frac{2\pi}{T}} \tag{VII}
\end{gather}
\]
substituting expression (VII) into expression (VI), the speed will be
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{V(R,T,m)=2\pi \frac{R}{T}}
\end{gather}
\]
the speed will be dependent on radius R and period T and independent of mass m.To calculate the kinetic energy, we substitute the speed value found above into expression (I)
\[
\begin{gather}
K=\frac{m}{2}\left(2\pi\frac{R}{T}\right)^{2}\\
K=\frac{m}{2}4\pi^{2}\frac{R^{2}}{T^{2}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{K(R,T,m)=2\pi^{2}\frac{mR^{2}}{T^{2}}}
\end{gather}
\]
For the calculation of centripetal acceleration, we first substitute expression (VI) into expression (II)
\[
\begin{gather}
a_{cp}=\frac{(\omega R)^{2}}{R}\\
a_{cp}=\frac{\omega^{2}R^{\cancel{2}}}{\cancel{R}}
\end{gather}
\]
canceling the radius R and substituting the value of ω with the expression (VII)
\[
\begin{gather}
a_{cp}=\left(\frac{2\pi}{T}\right)^{2}R
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_{cp}(R,T,m)=\frac{4\pi^{2}R}{T^{2}}}
\end{gather}
\]
the value of the centripetal acceleration, like the speed, is independent of the mass m.
c) Substituting the result obtained above for the centripetal acceleration into the expression (V) for the force
\[
\begin{gather}
F=m\frac{4\pi^{2}R}{T^{2}}
\end{gather}
\]
multiplying the numerator and denominator on the right-hand side by R2
\[
\begin{gather}
F=m\frac{4\pi^{2}R}{T^{2}}\times\frac{R^{2}}{R^{2}}\\[5pt]
F=m\frac{4\pi^{2}R^{3}}{T^{2}R^{2}}\\[5pt]
F=4\pi^{2}\frac{R^{3}}{T^{2}}\frac{m}{R^{2}}
\end{gather}
\]
In this expression the factor 4π2 is constant, and the factor
\( \dfrac{R^{3}}{T^{2}} \)
is also constant, remembering Kepler's Third Law: "The ratio between the cube of the distance of a
planet from the Sun and the square of the period remains constant for any planet". Then these two factors
form a new constant that can be defined as
\[
\begin{gather}
A\equiv 4\pi^{2}\frac{R^{3}}{T^{2}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F=A\frac{m}{R^{2}}}
\end{gather}
\]
d) To calculate the centripetal acceleration, we use expression (II) with the data for the Earth
\[
\begin{gather}
a_{cp}=\frac{V_{T}^{2}}{R_{T}}\\[5pt]
a_{cp}=\frac{\left(3\times 10^{4}\right)^{2}}{15\times 10^{10}}\\[5pt]
a_{cp}=\frac{9\times 10^{8}}{15\times 10^{10}}\\[5pt]
a_{cp}=\frac{9\times 10^{8}\times 10^{-10}}{15}\\[5pt]
a_{cp}=\frac{9\times 10^{-2}}{15}\\[5pt]
a_{cp}=0.006
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{a_{cp}=6\times 10^{-3}\;\text{m/s}}
\end{gather}
\]
The force is obtained using the expression (V), and the acceleration calculated above
\[
\begin{gather}
F=m_{T}a_{cp}\\[5pt]
F=6\times 10^{24}\times 6\times 10^{-3}\\[5pt]
F=36\times 10^{21}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F=3.6\times 10^{22}\;\text{N}}
\end{gather}
\]
The kinetic energy is calculated using the result of part (a) and the force calculated above
\[
\begin{gather}
K=\frac{FR}{2}\\[5pt]
K=\frac{3.6\times 10^{22}\times 15\times 10^{10}}{2}\\[5pt]
K=\frac{54\times 10^{32}}{2}\\[5pt]
K=27\times 10^{32}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{K=2.7\times 10^{33}\;\text{J}}
\end{gather}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .