Exercice Résolu sur les Dynamique
publicité
- Solution 2 du problème:
\[
\begin{gather}
\bbox[5px,border:5px solid #99CCFF]
{v^2(x)=-4x^2+100} \tag{I}
\end{gather}
\]
- Solution 3 du problème:
\[
\begin{gather}
x(t)=5\operatorname{sen}2t \tag{II}
\end{gather}
\]
\[
\begin{gather}
v(t)=10\cos 2t \tag{III}
\end{gather}
\]
en isolant le temps t dans l'équation (II)
\[
\begin{gather}
t=\frac{1}{2}\operatorname{arcsen}\frac{x}{5}
\end{gather}
\]
En substituant cette valeur dans l'équation (III), on obtient l'équation de la vitesse en fonction de la
position v(x)
\[
\begin{gather}
v=10\cos 2t\\[5pt]
v=10\cos\left(\cancel 2\times\frac{1}{\cancel 2}\operatorname{arcsen}\frac{x}{5}\right)
\end{gather}
\]
\[
\begin{gather}
\bbox[5px,border:5px solid #99CCFF]
{v(x)=10\cos\left(\operatorname{arcsen}\frac{x}{5}\right)} \tag{IV}
\end{gather}
\]
Nous allons montrer que l'équation (IV) est égale à l'équation (I).Dans l'équation (IV), en définissant θ comme
\[
\begin{gather}
\theta=\operatorname{arcsen}\frac{x}{5}\\[5pt]
\operatorname{sen}\theta=\frac{x}{5}\\[5pt]
\operatorname{sen}\theta=\frac{\frac{x}{5}}{1}
\end{gather}
\]
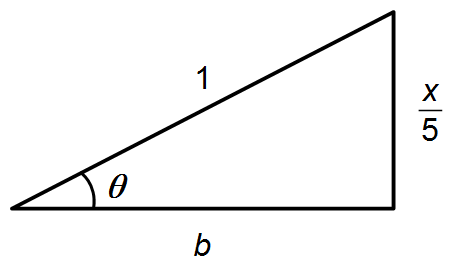
θ est l'angle d'un triangle rectangle avec une hypotenuse égale à 1 et des côtés égaux à
\( \left(\frac{x}{5}\right) \)
et b (Figure 1).
En appliquant le Théorème de Pythagore, nous trouvons la valeur du côté b
En appliquant le Théorème de Pythagore, nous trouvons la valeur du côté b
\[
\begin{gather}
h^2=a^2+b^2\\[5pt]
1^2=\left(\frac{x}{5}\right)^2+b^2\\[5pt]
b=\sqrt{1-\left(\frac{x}{5}\right)^2\;}
\end{gather}
\]
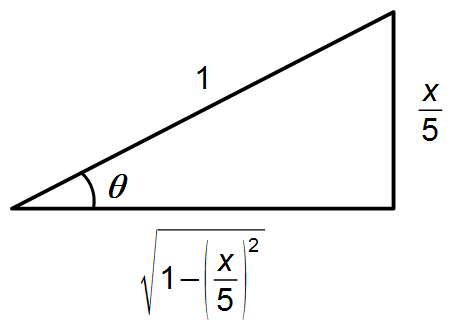
Le cosinus de l'angle θ est donné par (Figure 2)
\[
\begin{gather}
\cos\theta=\frac{b}{1}=\frac{\sqrt{1-\left(\frac{x}{5}\right)^2\;}}{1}\\[5pt]
\cos\left(\operatorname{arcsen}\frac{x}{5}\right)=\sqrt{1-\frac{x^2}{25}\;} \tag{V}
\end{gather}
\]
\[
\begin{gather}
v=10\sqrt{1-\frac{x^2}{25}\;}\\[5pt]
v^2=\left(10\sqrt{1-\frac{x^2}{25}\;}\right)^2\\[5pt]
v^2=100\left(1-\frac{x^2}{25}\right)\\[5pt]
v^2=100\left(\frac{25-x^2}{25}\right)\\[5pt]
v^2=4(25-x^2)\\[5pt]
\qquad\qquad v^2=100-4x^2\qquad (:2)\\[5pt]
\frac{v^2}{2}=\frac{100}{2}-\frac{4x^2}{2}\\[5pt]
\frac{v^2}{2}=\frac{-{4x^2}}{2}+50
\end{gather}
\]
Et l'équation trigonométrique (IV) est égale à l'équation algébrique (I), elles représentent le même
système physique.
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .