Exercice Résolu sur les Champ Électrique
EN
ES
PT-BR
publicité
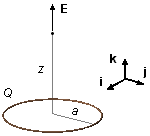
Un anneau de rayon a est chargé uniformément avec une charge Q. Calculer le vecteur champ
électrique en un point P l'axe de symétrie perpendiculaire au plan de l'anneau à une distance
z de son centre.
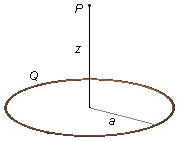
Données du problème:
- Rayon de l'anneau: a;
- Charge de l'anneau: Q;
- Distance au point où l'on veut le champ électrique: z.
Le vecteur position r va d'un élément de charge de l'anneau dq jusqu'au point P où voulons-nous calculer le champ électrique, le vecteur rq localise l'élément de charge par rapport à l'origine du référentiel et le vecteur rp localise le point P (Figure 1-A).
\[
\begin{gather}
\mathbf r=\mathbf r_p-\mathbf r_q
\end{gather}
\]
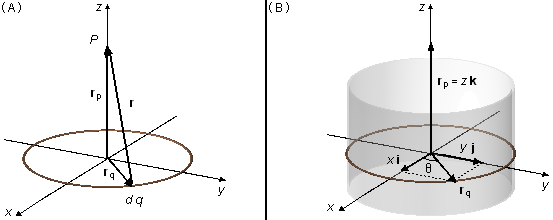
Par la géométrie du problème, nous choisissons des coordonnées cylindriques (Figure 1-B), le vecteur rq, se trouve dans le plan xy, est écrit comme \( \mathbf r_q=x\;\mathbf i+y\;\mathbf j \) et le vecteur rp n'a qu'une composante dans la direction k, \( \mathbf r_p=z\;\mathbf k \), le vecteur position sera
\[
\begin{gather}
\mathbf r=z\;\mathbf k-\left(x\;\mathbf i+y\;\mathbf j\right)\\[5pt]
\mathbf r=-x\;\mathbf i-y\;\mathbf j+z\;\mathbf k \tag{I}
\end{gather}
\]
De l'équation (I), le module du vecteur position r sera
\[
\begin{gather}
r^2=(-x)^2+(-y)^2+z^2\\[5pt]
r=\left(x^2+y^2+z^2\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
où x, y et z, en coordonnées cylindriques, sont donnés par
\[
\begin{gather}
\left\{
\begin{array}{l}
x=a\cos\theta\\
y=a\sin\theta\\
z=z
\end{array}
\right. \tag{III}
\end{gather}
\]
Solution:
Le vecteur champ électrique est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{dq}{r^2}\;\frac{\mathbf r}{r}}}
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{dq}{r^3}\;\mathbf r} \tag{IV}
\end{gather}
\]
En utilisant l'équation de la charge linéique λ, nous obtenons l'élément de charge dq
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\end{gather}
\]
\[
\begin{gather}
dq=\lambda\;ds \tag{V}
\end{gather}
\]
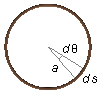
où ds est un élément d'arc d'angle dθ de l'anneau (Figure 2)
\[
\begin{gather}
ds=a\;d\theta \tag{VI}
\end{gather}
\]
en substituant l'équation (VI) dans l'équation (V)
\[
\begin{gather}
dq=\lambda a\;d\theta \tag{VII}
\end{gather}
\]
En substituant les équations (I), (II) et (VII) dans l'équation (IV)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[\left(x^2+y^2+z^2\right)^{1/2}\right]^3}}\left(-x\;\mathbf i-y\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left(x^2+y^2+z^2\right)^{3/2}}}\left(-x\;\mathbf i-y\;\mathbf j+z\;\mathbf k\right) \tag{VIII}
\end{gather}
\]
en substituant les équations de (III) dans l'équation (VIII)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[\left(a\cos\theta\right)^2+\left(a\sin\theta\right)^2+z^2\right]^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\sin\theta\;\mathbf j+z\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[a^2\cos^2\theta +a^2\sin^2\theta+z^2\right]^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\sin\theta\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left[a^2\underbrace{\left(\cos^2\theta +\sin^2\theta\right)}_{1}+z^2\right]^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\sin\theta\;\mathbf j+z\;\mathbf k\right)\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\int{\frac{\lambda a\;d\theta}{\left(a^2+z^2\right)^{3/2}}}\left(-a\cos\theta\;\mathbf i-a\sin\theta\;\mathbf j+z\;\mathbf k\;\right)
\end{gather}
\]
Comme la densité de charge λ et le rayon a sont constants, ils peuvent sortir de
l'intégrale, et étant l'intégrale de la somme égale à la somme des intégrales
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(a^2+z^2\right)^{3/2}}\left(-a\int\cos\theta\;d\theta\;\mathbf i-a\int\sin\theta\;d\theta\;\mathbf j+z\int\;d\theta\;\mathbf k\;\right)
\end{gather}
\]
L'íntervalle d'intégration sera 0 et 2π (un tour complet de l'anneau)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(a^2+z^2\right)^{3/2}}\left(-a\underbrace{\int_0^{2\pi}\cos\theta\;d\theta}_0\;\mathbf i-a\underbrace{\int_0^{2\pi}\sin\theta\;d\theta}_0\;\mathbf j+z\int_0^{2\pi}\;d\theta\;\mathbf k\right)
\end{gather}
\]
Intégrale de \( \displaystyle \int_0^{2\pi}\cos\theta\;d\theta \)
1ère méthode
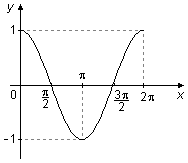Figure 3
1ère méthode
\[
\begin{align}
\int_0^{2\pi}\cos\theta\;d\theta &=\left.\sin\theta\;\right|_{\;0}^{\;2\pi}=\sin2\pi-\sin0=\\
&=0-0=0
\end{align}
\]
2ème méthode
Le graphique du cosinus entre 0 et 2π a une aire "positive" au-dessus de l'axe x entre 0 et \( \frac{\pi}{2} \) et entre \( \frac{3\pi}{2} \) et 2π, et une aire "négative" en dessous de l'axe x entre \( \frac{\pi}{2} \) et \( \frac{3\pi}{2} \), ces deux aires se compensent dans le calcul de l'intégrale et la valeur de l'intégrale est nulle (Figure 3).
Le graphique du cosinus entre 0 et 2π a une aire "positive" au-dessus de l'axe x entre 0 et \( \frac{\pi}{2} \) et entre \( \frac{3\pi}{2} \) et 2π, et une aire "négative" en dessous de l'axe x entre \( \frac{\pi}{2} \) et \( \frac{3\pi}{2} \), ces deux aires se compensent dans le calcul de l'intégrale et la valeur de l'intégrale est nulle (Figure 3).
Intégrale de \( \displaystyle \int_0^{2\pi}\sin\theta\;d\theta \)
1ère méthode
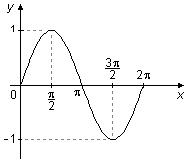Figure 4
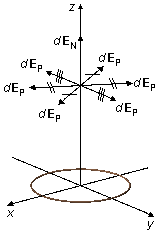Figure 5
1ère méthode
\[
\begin{align}
\int_0^{2\pi}\sin\theta\;d\theta &=\left.-\cos\theta\;\right|_{\;0}^{\;2\pi}=-(\cos 2\pi-\cos 0)=\\
&=-(1-1)=0
\end{align}
\]
2ème méthode
Le graphique du sinus entre 0 et 2π a une aire "positive" au-dessus de l'axe x entre 0 et π et une aire "négative" en dessous de l'axe x entre π et 2π, ces deux aires se compensent dans le calcul de l'intégrale et la valeur de l'intégrale est nulle (Figure 4).
Le graphique du sinus entre 0 et 2π a une aire "positive" au-dessus de l'axe x entre 0 et π et une aire "négative" en dessous de l'axe x entre π et 2π, ces deux aires se compensent dans le calcul de l'intégrale et la valeur de l'intégrale est nulle (Figure 4).
Remarque: les deux intégrales, dans les directions i et j, étant nulles,
représentent le calcul mathématique pour l'affirmation couramment faite que les composantes du champ
électrique parallèles au plan xy (dEP) s'annulent. Seules les
composantes normales au plan (dEN) contribuent au champ électrique
total (Figure 5).
Intégrale de \( \displaystyle \int_0^{2\pi}d\theta \)
\[
\begin{gather}
\int_0^{2\pi}d\theta =\left.\theta\;\right|_{\;0}^{\;2\pi}=2\pi-0=2\pi
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{\lambda a}{\left(a^2+z^2\right)^{3/2}}2\pi z\;\mathbf k\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2\pi\lambda a z}{\left(a^2+z^2\right)^{3/2}}\;\mathbf k \tag{IX}
\end{gather}
\]
La charge totale de l'anneau est Q et sa longueur est 2πa, la charge linéique peut être
écrite
\[
\begin{gather}
\lambda =\frac{Q}{2\pi a}\\[5pt]
Q=2\pi a\lambda \tag{X}
\end{gather}
\]
en substituant l'équation (X) dans l'équation (IX)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{Qz}{\left(a^2+z^2\right)^{3/2}}\;\mathbf k}
\end{gather}
\]
publicité
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .