Exercice Résolu sur les Mouvement Unidimensionnel
publicité   



Un passager est à 5 m de distance et court pour essayer d'attraper un train qui part du repos avec une accélération de 2 m/s2. Quelle doit être la vitesse constante minimale du passager, vp, pour atteindre le train?




Données du problème:
  • Distance du passager au train:    d = 5 m;
  • Vitesse initiale du train:    v0t = 0;
  • Accélération du train:    a = 2 m/s2.
Schéma du problème:

Ce problème peut être réduit à deux points matériels représentant le passager et la porte du train. Nous choisissons un référencel au point où se trouve le passager. La position initiale du passager est S0p = 0 et la position initiale du train est S0t = 8 m (Figure 1).
Figure 1

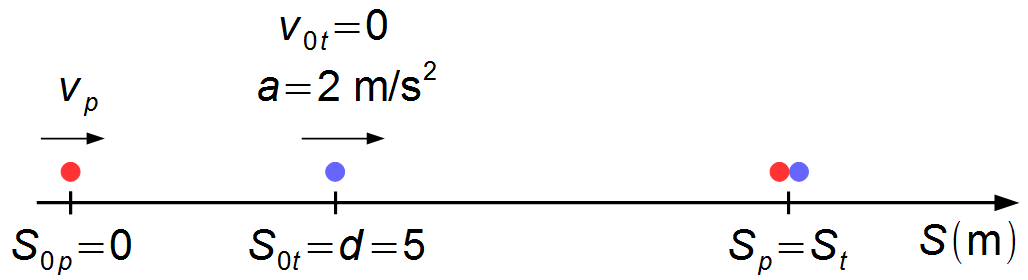
Solution

Le passager court avec une vitesse constante, il est en Mouvement Rectiligne Uniforme (MRU), donné par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t} \end{gather} \]
\[ \begin{gather} S_p=S_{0p}+v_pt\\[5pt] S_p=0+v_pt\\[5pt] S_p=v_pt \tag{I} \end{gather} \]
Le train a une accélération constante, il est en Mouvement Rectiligne Uniformément Varié (MRUV), donné par
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}t^2} \end{gather} \]
\[ \begin{gather} S_t=S_{0t}+v_{0t}+\frac{a}{2}t^2\\[5pt] S_t=5+0\times t+\frac{a}{2}t^2\\[5pt] S_t=5+t^2 \tag{II} \end{gather} \]
Pour que le passager atteigne la porte du train, nous devons imposer la condition d'égalité des équations (I) et (II)
\[ \begin{gather} S_p=S_t\\[5pt] v_pt=5+t^2\\[5pt] t^2-v_pt+5=0 \end{gather} \]
C'est une Équation du Second Degré en t.

Solution de l'équation    \( t^2-v_pt+5=0 \)

\[ \begin{gather} \Delta =b^2-4ac=v_p^2-4\times 1\times 5=v_p^2-20 \end{gather} \]
\[ \begin{gather} t=\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-v_p\pm\sqrt{v_p^2-20\;}}{2\times 1} \end{gather} \]

Pour que l'équation ait des racines réelles, nous devons avoir \( \Delta \geqslant 0\Rightarrow v_p^2-20\geqslant 0 \)
\[ \begin{gather} v_p^2-20\geqslant 0\\[5pt] v_p^2\geqslant20\\[5pt] v_p\geqslant \sqrt{20\;} \end{gather} \]
La vitesse minimale du passager pour monter dans le train sera
\[ \begin{gather} \bbox[#FFCCCC,10px] {v_p\simeq 4,5\;\mathrm{m/s}} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .