Exercice Résolu sur les Champ Électrique
publicité
Considérer deux charges égales de même signe séparées par une distance 2d. Calculer le module du champ électrique aux points situés le long de la médiatrice de la droite qui relie les deux charges. Vérifier la solution pour des points loin du centre des charges.
Construction du vecteur champ électrique résultant:
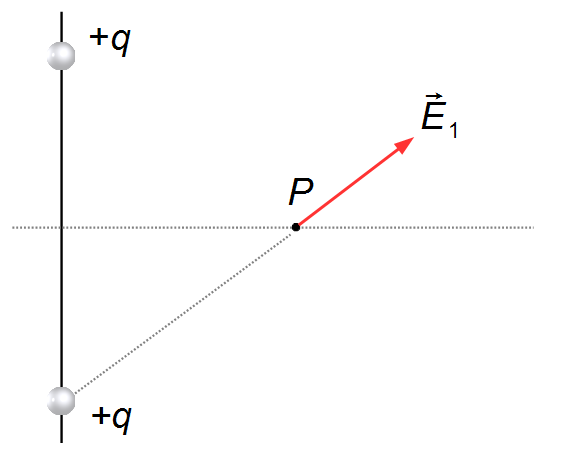
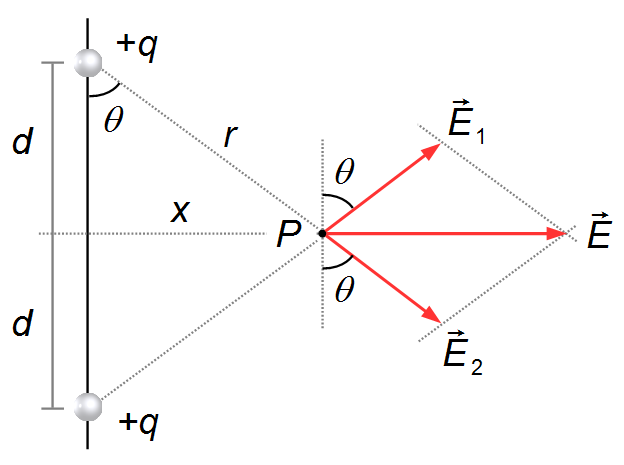
Sur la médiatrice de la droite qui relie les charges, nous choisissons un point P quelconque où
nous voulons calculer le champ électrique. Dans la direction du segment de droite reliant l'une des
charges +q au point P, nous traçons le vecteur
\( \vec E_1 \)
pointant vers l'extérieur de la charge, q>0 (Figure 1).
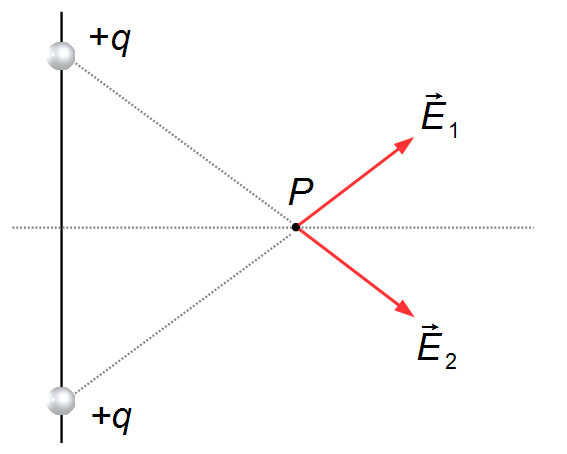
Dans la direction du segment de droite reliant l'autre charge +q au point P, nous traçons
le vecteur
\( \vec E_2 \)
pointant vers l'extérieur de la charge, q>0 (Figure 2).
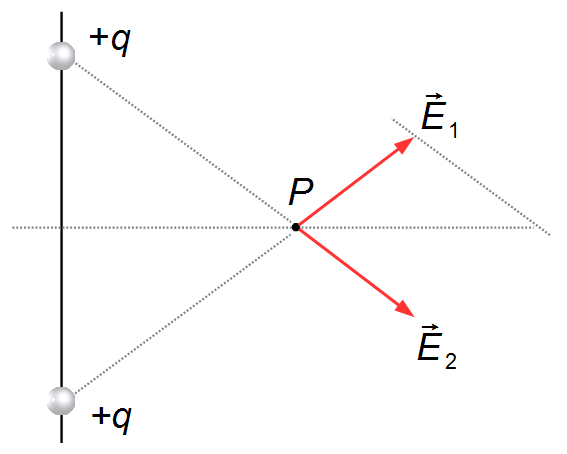
Nous traçons par l'extrémité du vecteur
\( \vec E_1 \)
une droite parallèle au vecteur
\( \vec E_2 \)
(Figure 3).
Nous traçons par l'extrémité du vecteur
\( \vec E_2 \)
une droite parallèle au vecteur
\( \vec E_1 \)
(Figure 4).
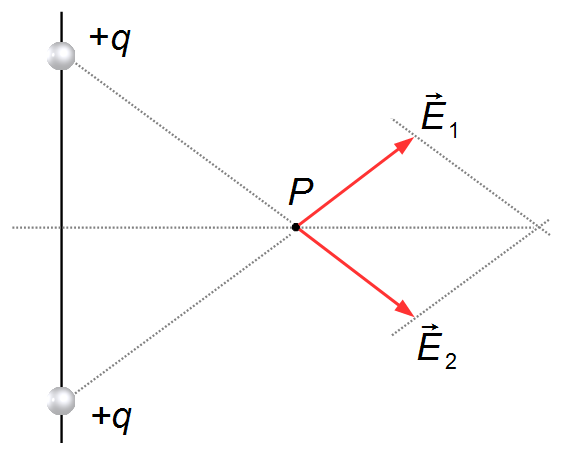
Du point P à l'intersection des droites, nous obtenons le vecteur résultant
\( \vec E \),
l'angle θ étant l'angle entre le vecteur champ électrique
\( \vec E_2 \)
(ou le vecteur
\( \vec E_1 \)
) et une droite auxiliaire verticale parallèle à la droite reliant les deux charges. L'angle
θ que les vecteurs champ électrique,
\( \vec E_1 \)
et
\( \vec E_2 \),
forment avec la droite auxiliaire est le même angle que le segment r forme avec le segment
vertical d (Figure 5).
Remarque 1: ce système ne représente pas un dipôle électrique, un dipôle
est formé par des charges de même valeur mais de signes opposés, alors qu'ici nous avons
des charges de même signe.
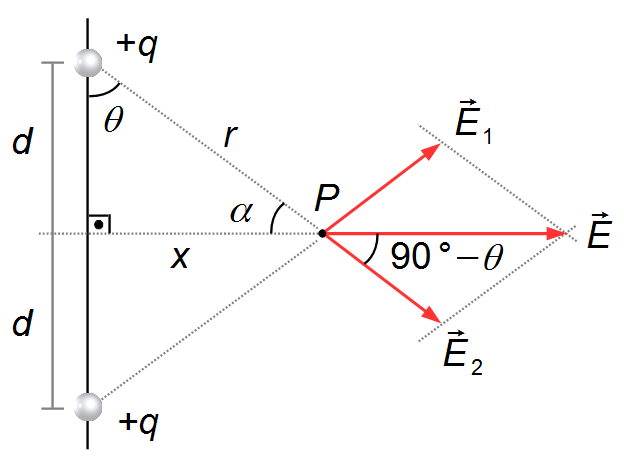 Figure 6
Figure 6
Remarque 2: au lieu d'utiliser l'angle θ entre le segment r et le
segment vertical d entre les deux charges, nous pourrions utiliser l'angle entre le segment
r et le segment x (Figure 6). La somme des angles intérieurs d'un triangle est égale à
180°
\[
\begin{gather}
180°=90°+\theta+\alpha\\[5pt]
\alpha=90°\theta
\end{gather}
\]

Solution:
Le module du champ électrique de chaque charge est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E=k_e\frac{q}{r^2}} \tag{I}
\end{gather}
\]
Le champ électrique résultant sera donné par
\[
\begin{gather}
\vec E=\vec E_1+\vec E_2
\end{gather}
\]
comme les charges ont la même valeur, en module
\( E_1=E_2 \)
\[
\begin{gather}
E=E_1\sin\theta+E_2\sin\theta\\[5pt]
E=2E_1\sin\theta \tag{II}
\end{gather}
\]
Remarque: en utilisant le cos 90°−θ obtenu ci-dessus, le champ
électrique sera
\[
\begin{gather}
E=2E_1\;\cos(90°-\theta)
\end{gather}
\]
le cosinus de la différence des arcs est donné par
\[
\begin{gather}
\cos (a-b)=\cos a\cos b+\sin a\sin b\\[10pt]
\cos (90°-\theta)=\underbrace{\cos90°}_0\cos\theta+\underbrace{\sin90°}_1\sin\theta\\[5pt]
\cos(90°-\theta)=\sin\theta
\end{gather}
\]
Le sinus de θ est obtenu à partir de r et x
\[
\begin{gather}
\sin\theta=\frac{x}{r} \tag{III}
\end{gather}
\]
le segment r est obtenu en utilisant le Théorème de Pythagore
\[
\begin{gather}
r^2=d^2+x^2\\[5pt]
r=\sqrt{d^2+x^2\;} \tag{IV}
\end{gather}
\]
en substituant l'équation (IV) dans l'équation (III)
\[
\begin{gather}
\sin\theta=\frac{x}{\sqrt{d^2+x^2\;}} \tag{V}
\end{gather}
\]
En substituant les équations (I) et (V) dans l'équation (II)
\[
\begin{gather}
E=2k_e\frac{q}{\left(\sqrt{d^2+x^2\;}\right)^2}\frac{x}{\sqrt{d^2+x^2\;}}\\[5pt]
E=2k_e\frac{q}{\left(d^2+x^2\right)}\frac{x}{\left(d^2+x^2\right)^{\frac{1}{2}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{2k_eqx}{\left(d^2+x^2\right)^{\frac{3}{2}}}}
\end{gather}
\]
Pour des points loin du centre du dipôle, nous avons x≫d, on peut négliger le terme en
d2 dans le dénominateur et la solution sera
\[
\begin{gather}
E=\frac{2k_eqx}{x^{{\cancel 2}\times{\frac{3}{\cancel 2}}}} \\[5pt]
E=\frac{2k_eq\cancel x}{x^{\cancelto{2}{3}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{2k_eq}{x^2}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .