Exercice Résolu sur les Champ Électrique
publicité   



Deux charges ponctuelles, de 5×10−6 C et 3×10−6 C, occupent deux sommets d'un triangle équilatéral de 1,2 m de côté. Calculer le module du champ électrique au troisième sommet en supposant que le milieu soit le vide.


Données du problème:
  • Charge 1:    q1 = 5×10−6 C;
  • Charge 2:    q2 = 3×10−6 C;
  • Distance entre les charges:    d = 1,2 m;
  • Constante de Coulomb dans le vide:    \( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).
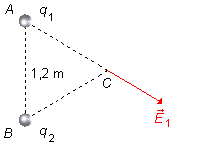
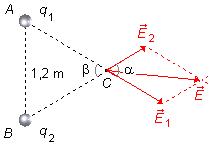
Construction du vecteur champ électrique résultant:

Les charges q1 et q2 sont situées aux sommets A et B du triangle. En considérant la charge q1 de valeur plus élevée 5×10−6 C, traçons au point C le vecteur \( \vec E_1 \), dans la direction du segment \( \overline{AC} \), avec un sens pointant vers l'extérieur de la charge, q > 0. La charge de plus grande valeur produit un champ plus intense (Figure 1).
Figure 1

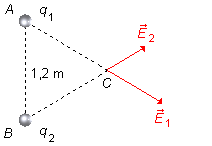
Au point C, traçons le vecteur \( \vec E_2 \), dans la direction du segment \( \overline{BC} \), avec un sens vers l'extérieur et de taille moindre, la charge q2 est de valeur plus faible, 3×10−6 C, et produit un champ moins intense (Figure 2).
Figure 2

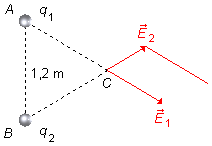
Traçons, depuis l'extrémité du vecteur \( \vec E_2 \), une ligne parallèle au vecteur \( \vec E_1 \) (Figure 3).
Figure 3

Traçons, depuis l'extrémité du vecteur \( \vec E_1 \), une ligne parallèle au vecteur \( \vec E_2 \) (Figure 4).
Figure 4

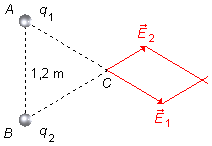
Depuis le sommet C jusqu'à l'intersection des lignes, nous obtenons le vecteur résultant \( \vec E \), où α est l'angle entre les vecteurs champ électrique \( \vec E_1 \) et \( \vec E_2 \). Comme le triangle est équilatéral, tous ses angles internes sont égaux à β = 60°. Comme les angles α et β sont opposés par le sommet, l'angle α vaut également 60° (Figure 5).
Figure 5

Solution:

Le champ électrique résultant est donné par
\[ \begin{gather} \vec E=\vec E_1+\vec E_2 \end{gather} \]
en module, et peut être calculé en utilisant la Loi des Cosinus
\[ \begin{gather} \bbox[#99CCFF,10px] {E^2=E_1^2+E_3^2+2E_1E_2\cos\alpha} \tag{I} \end{gather} \]
Le module du champ électrique de chaque charge est calculé par
\[ \begin{gather} \bbox[#99CCFF,10px] {E=k_e\frac{q}{r^2}} \end{gather} \]
\[ \begin{gather} E_1=k_e\frac{q_1}{r_1^2}\\[5pt] E_1=9\times 10^9\times \frac{5\times 10^{-6}}{(1,2)^2}\\[5pt] E_1=\frac{4,5\times 10^4}{1,44}\\[5pt] E_1\approx 3,1\times 10^4\;\mathrm{\frac{N}{C}} \tag{II} \end{gather} \]
\[ \begin{gather} E_2=k_e\frac{q_2}{r_2^2}\\[5pt] E_2=9\times 10^9\times \frac{3\times 10^{-6}}{(1,2)^2}\\[5pt] E_2=\frac{2,7\times 10^4}{1,44}\\[5pt] E_2\approx 1,9\times 10^4\;\mathrm{\frac{N}{C}} \tag{III} \end{gather} \]
en substituant les équations (II) et (III) dans l'équation (I)
\[ \begin{gather} E^2=(3,1\times 10^4)^2+(1,9\times 10^4)^2+2.3,1\times 10^4\times 1,9\times 10^4\cos60°\\[5pt] E^2=9,6\times 10^8+3,6\times 10^8+\cancel 2\times 5,9.10^8\times \frac{1}{\cancel 2}\\[5pt] E^2=(9,6+3,6+5,9)\times 10^8\\[5pt] E^2=19,1\times 10^8\\[5pt] E=\sqrt{19,1\times 10^8\;} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {E\approx 4,4\times 10^4\;\mathrm{\frac{N}{C}}} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .