Pendant un brouillard, un navigateur reçoit deux signaux émis simultanément par un poste sur la côte, l'un à travers l'air et l'autre à travers l'eau. Entre les réceptions des deux sons, il s'écoule un intervalle de temps Δt=5 secondes. Dans les conditions de l'expérience, la vitesse du son est de 341 m/s dans l'air et de 1504 m/s dans l'eau. Déterminer la distance x entre le bateau et le poste émetteur des signaux.


Données du problème:

• Vitesse du son dans l'air:    v_a = 341 m/s;
• Vitesse du son dans l'eau:    v_e = 1504 m/s;
• Intervalle de temps entre les réceptions:    Δt = 5 s.

Schéma du problème:

Comme l'onde sonore qui se propage dans l'eau a une vitesse plus élevée, elle arrive plus tôt au bateau. Soit t le temps de propagation de l'onde dans l'eau, et t+Δt le temps de propagation de l'onde dans l'air (ce sera la somme du temps t de propagation dans l'eau avec le retard Δt dû à sa propagation plus lente).


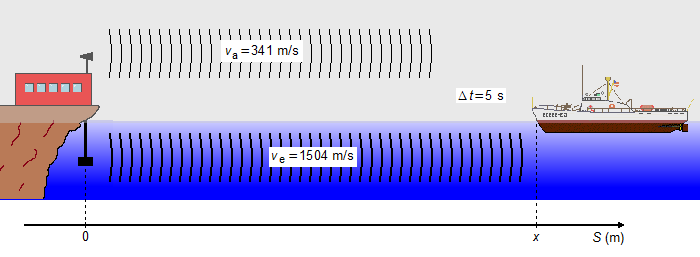
Nous choisissons un référentiel orienté vers la droite avec l'origine à la position d'émission du son. La position initiale des ondes sonores sera S_0a = S_0e = 0, la position du bateau est x, la position finale où les ondes doivent arriver est S_a = S_e = x.

Solution

Comme les ondes ont une vitesse constante, elles sont en Mouvement Rectiligne Uniforme donné par En appliquant l'équation (I) pour l'onde qui se propage dans l'eau En appliquant l'équation (I) pour l'onde qui se propage dans l'air De l'équation (II), nous pouvons isoler la valeur de t en remplaçant l'expression (IV) dans l'équation (III) en multipliant les deux côtés de l'égalité par 1504