Mouvement Unidimensionnel
publicité
Une pierre est lancée, avec une vitesse initiale de 15 m/s, du sommet d'une falaise de 20 m de hauteur,
simultanément une autre pierre est lancée verticalement depuis le bas de la falaise vers le haut également
avec une vitesse de 15 m/s. Déterminer:
a) Après combien de temps et à quelle hauteur les pierres se croisent-elles ?
b) La pierre lancée d'en bas atteint-elle le sommet de la falaise?
a) Après combien de temps et à quelle hauteur les pierres se croisent-elles ?
b) La pierre lancée d'en bas atteint-elle le sommet de la falaise?
Une fusée est lancée verticalement depuis le sol avec une vitesse initiale de 200 m/s. Après 10 secondes,
elle explose. Un observateur au sol situé à une distance de 2000 mètres, sur la même ligne horizontale que
le point de lancement. Au bout de combien de temps l’observateur entend-il le bruit de l’explosion? La
vitesse du son dans l'air est de 340 m/s.
Sur la Lune, une pierre est abandonnée d'une hauteur de 20 mètres à partir du repos. Elle tombe sous
l'action de l'accélération de la pesanteur lunaire jusqu'à ce qu'elle atteigne le sol avec une vitesse
v. Déterminer à quelle hauteur la pierre doit être abandonnée sur Terre pour qu'elle atteigne le
sol avec la même vitesse v. L'accélération de la pesanteur sur Terre est
gT = 9,8 m/s2, l'accélération de la pesanteur sur la Lune est
gL = 1,6 m/s2.
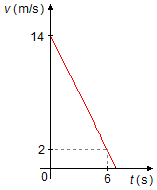
Le mouvement d'un corps est décrit par le graphique de la vitesse en fonction du temps comme illustré
dans la figure. Déterminer:
a) L'accélération du corps;
b) Écrire l'équation horaire de la vitesse;
c) Quelle est la distance parcourue entre 3 s et 7 s.
a) L'accélération du corps;
b) Écrire l'équation horaire de la vitesse;
c) Quelle est la distance parcourue entre 3 s et 7 s.
Le mouvement d'un corps est donné par le graphique de la vitesse en fonction du temps,
v = f(t):
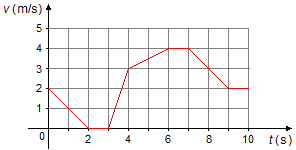
Déterminer:
a) L'espace parcouru entre 1 s et 9 s;
b) La vitesse moyenne entre 1 s et 9 s;
c) L'accélération moyenne entre 1 s et 9 s.
Un objet démarre avec une vitesse initiale de 1 m/s en mouvement rectiligne, le graphique de l'accélération
en fonction du temps depuis le début du mouvement est donné
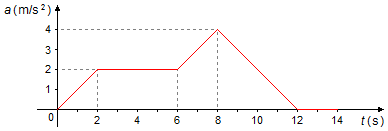
Déterminer:
a) La vitesse à t = 8 s;
b) La vitesse à t = 12 s;
c) La vitesse à t = 14 s;
d) Pendant quel intervalle de temps la vitesse diminue.
Étant donnée l'équation du mouvement
où la position S est mesuré en mètres et le temps t est mesuré en secondes, on demande:
a) Construis un tableau avec des valeurs pour t de 0 à 8 secondes, et à partir du tableau, construis le graphique de la fonction;
b) À quel instant le mobile passe-t-il par l'origine?
c) À quel instant le mobile change-t-il de sens?
S = 21 − 10 t + t2
où la position S est mesuré en mètres et le temps t est mesuré en secondes, on demande:
a) Construis un tableau avec des valeurs pour t de 0 à 8 secondes, et à partir du tableau, construis le graphique de la fonction;
b) À quel instant le mobile passe-t-il par l'origine?
c) À quel instant le mobile change-t-il de sens?
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .