Exercice Résolu sur les Mouvement Circulaire
publicité
Un garçon fait tourner au-dessus de sa tête une pierre attachée à une corde avec une vitesse linéaire
constante, le rayon décrit par la circonférence faite par la pierre est de 1 m et fait un tour en 2 s.
Déterminer:
a) La vitesse linéire de la pierre;
b) Le module de l'accélération centripète agissant sur la pierre.
a) La vitesse linéire de la pierre;
b) Le module de l'accélération centripète agissant sur la pierre.
Données du problème:
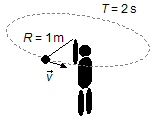
- Rayon de la trajectoire: R = 1 m;
- Période de rotation: T = 2 s.
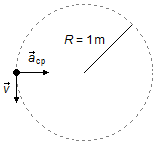
Schéma du problème:
Dans le système, nous avons la vitesse \( \vec v \) qui est tangente à la trajectoire, et l'accélération centripète \( {\vec a}_{cp} \) qui agit dans la direction de la corde, orientée vers le centre du cercle. L'accélération centripète est responsable de changer la direction de la vitesse linéaire (elle fait en sorte que la pierre tourne).
Solution
a) La vitesse linéaire est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{v=\omega r} \tag{I}
\end{gather}
\]
où ω est la vitesse angulaire donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega=\frac{2 \pi}{T}} \tag{II}
\end{gather}
\]
en remplaçant l'équation (II) dans l'équation (I)
\[
\begin{gather}
v=\frac{2 \pi}{T} r
\end{gather}
\]
en remplaçant les données du problème et en utilisant π = 3,14
\[
\begin{gather}
v =\frac{\cancel 2\times 3,14}{\cancel 2}\times 1
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v=3,14\;\mathrm{m/s}}
\end{gather}
\]
b) Le module de l'accélération centripète est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{|\;a_{cp}\;|=\frac{v^2}{r}}
\end{gather}
\]
\[
\begin{gather}
|\;a_{cp}\;|=\frac{3,14^2}{1}\\[5pt]
|\;a_{cp}\;|=\frac{9,86}{1}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{|\;a_{cp}\;|\approx 9,86\;\mathrm{m/s^2}}
\end{gather}
\]
publicité

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .