Exercice Résolu sur les Mécanique des Fluides
publicité   



Un ballon d'hydrogène pesant 600 N est attaché à un fil en équilibre statique vertical. Son volume est de 80 m3 et la densité de l'air est de 1,25 kg/m3. Déterminer:
a) La poussée due à l'air dans le ballon;
b) La tension dans le fil qui soutient le ballon;
c) L'accélération acquise par le ballon lorsque le fil se rompt.
Considérez la poussée de l'air comme constante.


Données du problème:
  • Poids du ballon:    P = 600 N;
  • Volume du ballon:    Vb = 80 m3;
  • Masse volumique de l'air:    ρar = 1,25 kg/m3;
  • Accélération de la pesanteur:    g = 9,8 m/s2.
Schéma du problème:

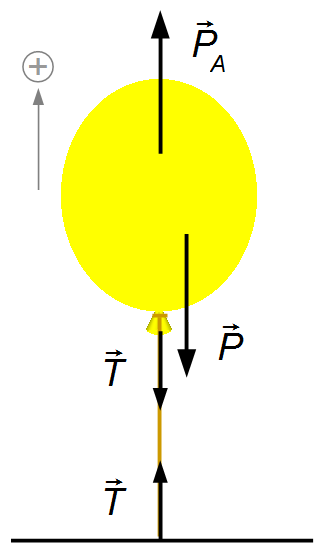
Sur le ballon agissent la force poids, \( \vec P \), la poussée due à l'air, \( {\vec P}_{\small A} \), et la force de tension de le fil, \( \vec T \), qui retient le ballon (Figure 1).
Figure 1

Solution

a) La poussée est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {P_{\small A}=m_{\small L} g} \tag{I} \end{gather} \]
où mL est la masse de liquide déplacée par le corps, dans ce cas l'air, mar.
La masse volumique est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {\rho=\frac{m}{V}} \end{gather} \]
avec le volume, V, du corps égal au volume d'air déplacé par le ballon, Vb, et ρ est la masse volumique de l'air, ρar.
\[ \begin{gather} m_{ar}=\rho_{ar}V_b \tag{II} \end{gather} \]
en substituant l'équation (II) dans l'équation (I)
\[ \begin{gather} P_{\small A}=\rho_{ar}V_b g\\[5pt] P_{\small A}=1,25\times 80\times 9,8 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {P_{\small A}=980\;\mathrm N} \end{gather} \]

b) Comme le ballon est en équilibre statique, la résultante des forces agissant sur le ballon est nulle
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum F=0} \end{gather} \]
Nous choisissons un référentiel pointant vers le haut (Figure 2), la résultante des forces sera
\[ \begin{gather} P_{\small A}-P-T=0\\[5pt] T=P_{\small A}-P\\[5pt] T=980-600 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T=380\;\mathrm N} \end{gather} \]
Figure 2

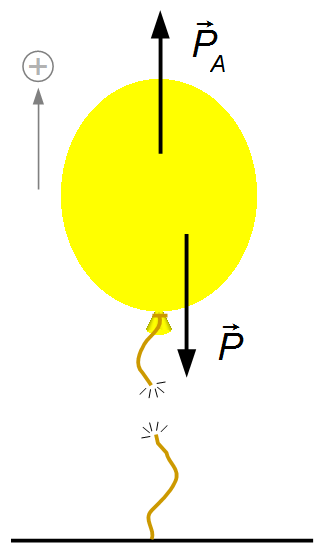
c) Lorsque le fil se rompt, la force de tension cesse d'exister et le ballon se déplace sous l'action de la force résultante entre le poids et la poussée (Figure 3). Choisissant un référentiel orienté vers le haut et appliquant la Deuxième Loi de Newton
\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
\[ \begin{gather} P_{\small A}-P=ma \tag{III} \end{gather} \]
Le poids du ballon est donnée par
\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]
Figure 3

la masse du ballon sera
\[ \begin{gather} m=\frac{P}{g} \tag{IV} \end{gather} \]
en substituant l'équation (IV) dans l'équation (III)
\[ \begin{gather} P_{\small A}-P=\frac{P}{g}a\\[5pt] a=(P_{\small A}-P)\frac{g}{P}\\[5pt] a=(980-600)\times\frac{9,8}{600}\\[5pt] \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=6,21\;\mathrm{m/s^2}} \end{gather} \]

Remarque: le problème nous demande de considérer la poussée de l'air comme constante, ce qui signifie que nous pouvons appliquer la Deuxième Loi de Newton avec une accélération constante. Dans une situation réelle, la densité de l'air diminue avec l'altitude, donc la force de poussée diminue également et n'est pas constante. Lorsque nous utilisons la Deuxième Loi de Newton avec une force variable, l'accélération n'est plus constante.
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .