Exercício Resolvido de Oscilações Harmônicas
publicidade
Um corpo de massa M está preso à extremidade de uma mola de massa mℓ que
oscila na vertical. Despreze a resistência do ar. Deternine:
a) A energia cinética da mola;
b) A energia cinética do sistema massa-mola;
c) O período de oscilação do sistema.
Calcule como função da constante elástica da mola (k), da massa do corpo (M) e da massa da mola (mℓ).
a) A energia cinética da mola;
b) A energia cinética do sistema massa-mola;
c) O período de oscilação do sistema.
Calcule como função da constante elástica da mola (k), da massa do corpo (M) e da massa da mola (mℓ).

Dados do problema:
- Massa do corpo: M;
- Massa da mola: mℓ;
- Constante elástica da mola: k .
A mola possui comprimento L e massa mℓ, podemos considerar que ela é composta por elementos de infinitesimais de comprimento ds e massa dmℓ (Figura 1-A).
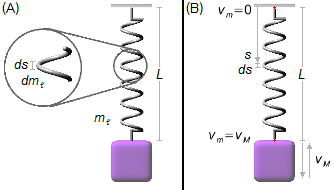
O bloco de massa M oscila com velocidade vM, o elemento da mola que se conecta ao bloco oscila com a mesma velocidade do bloco (vm = vM) e o elemento fixo no teto está em repouso (vm = 0). Cada elemento infinitesimal (ds) da mola tem sua posição descrita pelo ponto s, que varia de 0 (ponto fixo no teto) até L (ponto fixo na mola), Figura 1-B.
Observação: Não podemos substituir a mola por um corpo de massa mℓ oscilando
junto com o bloco. O bloco todo oscila com velocidade v, mas cada elemento da mola oscila com uma velocidade
diferente.
Solução
a) Da Figura 1-A podemos ter a seguinte relação entre massa e comprimento
\[
\begin{gather}
\frac{dm_{\ell}}{m_{\ell}}=\frac{ds}{L}\\
dm_{\ell}=\frac{m_{\ell}}{L}ds \tag{I}
\end{gather}
\]
Da Figura 1-B podemos ter a seguinte relação entre velocidade e deslocamento
\[
\begin{gather}
\frac{v_{m}}{v_{M}}=\frac{s}{L}\\
v_{m}=\frac{s}{L}v_{M} \tag{II}
\end{gather}
\]
Observação: Esta expressão é compatível com a situação apresentada na Figura 1-B
para s = 0
temos \( v_{m}=\dfrac{0}{L}v_{M}=0 \)
para s = L
temos \( v_{m}=\dfrac{L}{L}v_{M}=v_{M} \)
para s = 0
temos \( v_{m}=\dfrac{0}{L}v_{M}=0 \)
para s = L
temos \( v_{m}=\dfrac{L}{L}v_{M}=v_{M} \)
A energia cinética de um elemento de massa é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{dE_{c}=\frac{1}{2}v^{2}dm_{\ell}} \tag{III}
\end{gather}
\]
substituindo as expressões (I) e (II) na expressão (III), a energia cinética infinitesimal da mola
(dEcℓ) será
\[
\begin{gather}
dE_{c\ell}=\frac{1}{2}\left(\frac{s}{L}v_{M}\right)^{2}\frac{m_{\ell}}{L}ds\\[5pt]
dE_{c\ell}=\frac{1}{2}\frac{s^{2}}{L^{2}}v_{M}^{2}\frac{m_{\ell}}{L}ds\\[5pt]
dE_{c\ell}=\frac{1}{2}\frac{m_{\ell}v_{M}^{2}}{L^{3}}s^{2}ds
\end{gather}
\]
integrando de ambos os lados da igualdade, o fator 1/2 ,a massa da mola (mℓ),o comprimento
da mola (L) e a velocidade do bloco (vM) são constantes e saem da integral, os intervalos
de integração vão de 0 até Ecℓ, a energia do sistema, para
dEcℓ e de 0 a L para ds
\[
\begin{gather}
\int_{0}^{E_{c \ell}}{}dE_{c \ell}=\frac{1}{2}\frac{mv_{M}^{2}}{L^{3}}\int_{0}^{L}{}s^{2}\;ds\\[5pt]
E_{c\ell}=\frac{1}{2}\frac{mv_{M}^{2}}{L^{3}}\left.\frac{s^{3}}{3}\;\right|_{\;0}^{\;L}\\[5pt]
E_{c\ell}=\frac{1}{2}\frac{mv_{M}^{2}}{L^{3}}\frac{L^{3}-0^{3}}{3}\\[5pt]
E_{c\ell}=\frac{1}{2}\frac{mv_{M}^{2}}{\cancel{L^{3}}}\frac{\cancel{L^{3}}}{3}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{E_{c\ell}=\frac{1}{2}\left(\frac{m}{3}\right)v_{M}^{2}}
\]
Observação: Como foi escrito acima não se pode substitur a mola por um corpo de mesma massa da
mola. Pelo resultado encontrado vemos que o sistema oscila como se a mola fosse substituída por um corpo de
massa equivalente a um terço da massa da mola.
O sistema se comporta com se tivesssemos um bloco de massa M ligado a um bloco de massa mℓ/3 e uma mola de massa desprezível e oscilando com velocidade vM.
O sistema se comporta com se tivesssemos um bloco de massa M ligado a um bloco de massa mℓ/3 e uma mola de massa desprezível e oscilando com velocidade vM.
b) A energia do sistema será dada por
\[ \bbox[#99CCFF,10px]
{E_{c}=\frac{1}{2}mv^{2}}
\]
neste caso a massa será a massa efetiva (mef) do sistema dada pela soma da massa do bloco
(M) e da massa que substitui a mola
\( \left(\dfrac{m_{\ell}}{3}\right) \).
\[
m_{ef}=M+\frac{m_{\ell}}{3}
\]
\[
E_{c}=\frac{1}{2}m_{ef}v^{2}
\]
\[ \bbox[#FFCCCC,10px]
{E_{c}=\frac{1}{2}\left(M+\frac{m}{3}\right)v^{2}}
\]
c) O período das oscilações é dada por
\[ \bbox[#99CCFF,10px]
{T=2\pi \sqrt{\frac{m}{k}}}
\]
a massa considerada é a massa efetiva
\[ \bbox[#FFCCCC,10px]
{T=2\pi \sqrt{\frac{1}{k}\left(M+\frac{m}{3}\right)}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .