Exercício Resolvido de Regiões do Plano Complexo
publicidade
a) \( |z-z_{0}|\lt R \)
Sendo \( z=x+iy \) e \( z_{0}=x_{0}+iy_{0} \), temos
\[
\begin{gather}
|(x+iy)-(x_{0}+iy_{0})|\lt R\\
|x+iy-x_{0}-iy_{0}|\lt R\\
|x-x_{0}+iy-iy_{0}|\lt R\\
|(x-x_{0})+i(y-y_{0})|\lt R
\end{gather}
\]
o módulo de um número complexo é dado por
\[ \bbox[#99CCFF,10px]
{|z|=\sqrt{x^{2}+y^{2}}}
\]
calculando o módulo da expressão complexa e substituindo o sinal de “<” por “=”, obtemos
\[
\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}\;}=R
\]
elevando ao quadrado de ambos da igualdade
\[
\begin{gather}
\left(\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}\;}\right)^{2}=R^{2}\\
(x-x_{0})^{2}+(y-y_{0})^{2}=R^{2}
\end{gather}
\]
A expressão acima é a equação de uma circunferência de raio R e centrada no ponto
(x0, y0).
Então a expressão inicial representa, no plano complexo, uma circunferência de raio R centrada no ponto z0. Como queremos os pontos “menor que R” (<R) isto representa os pontos do interior da circunferência excluindo os pontos que sejam iguais a R (Figura 1).
Então a expressão inicial representa, no plano complexo, uma circunferência de raio R centrada no ponto z0. Como queremos os pontos “menor que R” (<R) isto representa os pontos do interior da circunferência excluindo os pontos que sejam iguais a R (Figura 1).
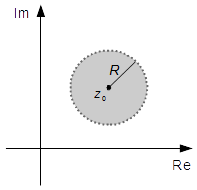
Figura 1
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .