Exercício Resolvido de Integral de Contorno
publicidade   



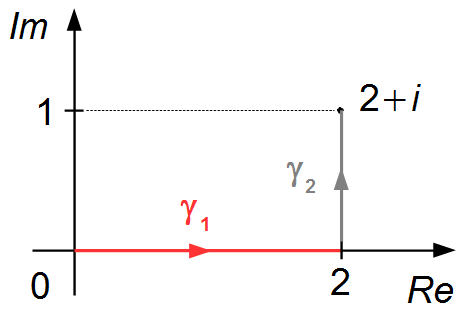
e) \( f(z)=y-x^{2} \),   ao longo do caminho formado por dois segmentos, o primeiro segmento que vai da origem ao ponto (2, 0), e o segundo segmento que vai do ponto (2, 0) ao ponto (2, 1).

A curva é formada por dois segmentos γ1 e γ2, que devem ser parametrizados separadamente.
A parametrização de uma reta é dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {z(t)=z_{1}+t(z_{2}-z_{1})} \end{gather} \]
  • Parametrização da curva γ1 (Figura 1)
Pontos inicial e final da curva,   \( z_{1}=0+0i \)   e   \( z_{2}=2+0i \)
\[ \begin{gather} z_{\gamma_{1}}(t)=(0+0i)+t[(2+0i)-(0+0i)]\\[5pt] \qquad \qquad \qquad \qquad z_{\gamma _{1}}(t)=2t\qquad ,\qquad \ 0\leqslant t\leqslant 1 \tag{I} \end{gather} \]
Figura 1
  • Derivada de   zγ1(t) = 2t
\[ \begin{gather} z'_{\gamma 1}(t)=\frac{dz_{\gamma 1}}{dt}=2 \tag{II} \end{gather} \]
A integral de contorno é dada por
\[ \begin{gather} \bbox[#99CCFF,10px] {\int f(z)\;dz=\int f(z(t))z'(t)\;dt} \end{gather} \]
  • Integral de   f(z)=y−x2
\[ \begin{gather} f(z)=y-x^{2} \tag{III} \end{gather} \]
Integral sobre a curva γ1
\[ \begin{gather} I_{1}=\int_{\gamma 1}f(z_{\gamma 1}(t))z'_{\gamma 1}(t)\;dt \tag{IV} \end{gather} \]
usando a expressão (I) obtemos f(zγ1(t))
\[ \begin{gather} z_{\gamma 1}(t)=\underbrace{\ 2t\ }_{x(t)}+\underbrace{\ 0\ }_{y(t)}i \tag{V} \end{gather} \]
substituindo os valores de x(t) e y(t) da expressão (V) na expressão (III)
\[ \begin{gather} f(z_{\gamma 1}(t))=0-(2t)^{2}\\ f(z_{\gamma1}(t))=-4t^{2} \tag{VI} \end{gather} \]
substituindo as expressões (II) e (VI) na expressão (IV)
\[ \begin{align} I_{1} &=\int_{0}^{1}(-4t^{2}).(2)\;dt=\int_{0}^{1}-8t^{2}\;dt=\\[5pt] &=-8\int_{0}^{1}t^{2}\;dt=-8.\;\left(\left.\frac{t^{3}}{3}\;\right|_{0}^{1}\right)=\\[5pt] &=-8.\left(\frac{1}{3}\right)=-{\frac{8}{3}} \tag{VII} \end{align} \]
  • Parametrização da curva γ2 (Figura 2)
Pontos inicial e final da curva,   \( z_{2}=2+0i \)   e   \( z_{3}=2+i \)
\[ \begin{gather} z_{\gamma_{2}}(t)=(2+0i)+t[(2+1i)-(2+0i)]\\[5pt] z_{\gamma_{2}}(t)=2+t[2+1i-2]\\[5pt] \qquad \qquad \qquad \qquad z_{\gamma_{2}}(t)=2+it\qquad ,\qquad 0\leqslant t\leqslant 1 \tag{VIII} \end{gather} \]
Figura 2
  • Derivada de   zγ2(t) = 2+it
\[ \begin{gather} z'_{\gamma 2}(t)=\frac{dz}{dt}=i \tag{IX} \end{gather} \]
  • Integral de   f(z)=y−x2
Integral sobre a curva γ2
\[ \begin{gather} I_{2}=\int_{\gamma 2}f(z_{\gamma 2}(t))z'_{\gamma 2}(t)\;dt \tag{X} \end{gather} \]
usando a expressão (VIII) obtemos f(zγ2(t))
\[ \begin{gather} z_{\gamma 2}(t)=\underbrace{\ 2\ }_{x(t)}+\underbrace{\ t\ }_{y(t)}i \tag{XI} \end{gather} \]
substituindo os valores de x(t) e y(t) da expressão (XI) na expressão (III)
\[ \begin{gather} f(z_{\gamma 2}(t))=t-(2)^{2}\\ f(z_{\gamma 2}(t))=t-4 \tag{XII} \end{gather} \]
substituindo as expressões (IX) e (XII) na expressão (X)
\[ \begin{align} I_{2} &=\int_{0}^{1}(t-4)(i)\;dt=\int_{0}^{1}(it-4i)\;dt= \\[5pt] &=i\int_{0}^{1}t\;dt-4i\int_{0}^{1}\;dt=i\left(\left.\frac{t^{2}}{2}\;\right|_{0}^{1}\right)-4i\left(\left.t\;\right|_{0}^{1}\right)=\\[5pt] &=i\left(\frac{1}{2}\right)-4i(1)=\frac{1}{2}i-4i=\frac{i-8i}{2}=-{\frac{7}{2}i}\tag{XIII} \end{align} \]
O resultado final será dado pela soma das integrais sobre os dois segmentos (VII) e (XIII)
\[ \begin{gather} I=I_{1}+I_{2}\\[5pt] I=-{\frac{8}{3}}-\frac{7}{2}i\\[5pt] I=\frac{-16-21i}{6} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {\int_{0}^{2+i}f(z)\;dz=-{\frac{16+21i}{6}}} \end{gather} \]
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .