Exercício Resolvido de Fórmula Integral de Cauchy
publicidade
b) \( \displaystyle \oint_{|z-1|=1}\frac{dz}{(z-1)^{3}(z+1)^{3}} \)
O caminho é dado pela circunferência de raio 1 com centro no ponto (1, 0), percorrida no sentido
anti-horário (Figura 1).
A Fórmula Integral de Cauchy na forma geral é dada por
A Fórmula Integral de Cauchy na forma geral é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{f^{(n)}(z_{0})=\frac{{n}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz} \tag{I}
\end{gather}
\]
Identificando os termos da integral
\[
\begin{gather}
\frac{{
\bbox[#FFCC66,2px]
{n}
}!}{2\pi \mathrm{i}}\;\oint_{{C}}\frac{
\bbox[#FFFF66,2px]
{f(z)}
}{\left(z-
\bbox[#FFD9CC,2px]
{z_{0}}
\right)^{
\bbox[#FFCC66,2px]
{n}
+1}}\;dz=\oint_{{|z-1|=1}}
\bbox[#FFFF66,2px]
{{\frac{1}{(z+1)^{3}}}}
\frac{1}{(z-
\bbox[#FFD9CC,2px]
{1}
)^{
\bbox[#FFCC66,2px]
{2}
+1}}\;dz
\end{gather}
\]
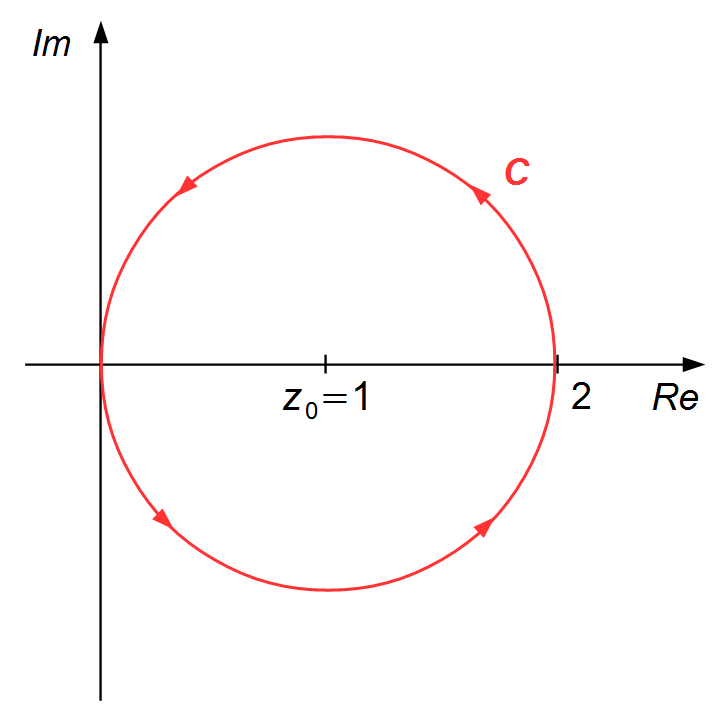
o ponto \( z-1=0\Rightarrow z=1 \) está no interior da região determinada pelo contorno C, ele será usado no cálculo da integral, temos \( f(z)=\frac{1}{(z+1)^{3}} \), z0 = 1 e n = 2, escrevendo a expressão (I)
\[
\begin{gather}
\oint_{{C}}\frac{f(z)}{\left(z-z_{0}\right)^{n+1}}\;dz=\frac{2\pi\mathrm{i}}{n!}\;f^{(n)}(z_{0})\\[5pt]
\oint_{|z-1|=1}\frac{dz}{(z-1)^{3}(z+1)^{3}}=\frac{2\pi\mathrm{i}}{2!}\;f^{(2)}(1)
\end{gather}
\]
Cálculo da derivada segunda de
\( \displaystyle f(z)=\frac{1}{(z+1)^{3}} \)
Rescrevendo a função f(z) como \( f(z)=(z+1)^{-3} \)
a função f(z) é uma função composta, usando a Regra da Cadeia
Rescrevendo a função f(z) como \( f(z)=(z+1)^{-3} \)
a função f(z) é uma função composta, usando a Regra da Cadeia
\[
\begin{gather}
\frac{du[v(z)]}{dz}=\frac{du}{dv}\frac{dv}{dz}
\end{gather}
\]
onde
\( u(v)=v^{-3} \)
e
\( v(z)=(z+1) \)
\[
\begin{gather}
\frac{df}{dz}=\frac{d\left(v^{-3}\right)}{dv}\frac{d(z+1)}{dz}\\[5pt]
\frac{df}{dz}=-3v^{-3-1}(1)\\[5pt]
\frac{df}{dz}=-3(z+1)^{-4}
\end{gather}
\]
derivando uma segunda vez, aplicando novamente a Regra da Cadeia, onde
\( u(v)=-3v^{-4} \)
e
\( v(z)=(z+1) \)
\[
\begin{gather}
\frac{d^{2}f}{dz^{2}}=\frac{d\left(-3v^{-4}\right)}{dv}\frac{d(z+1)}{dz}\\[5pt]
\frac{d^{2}f}{dz^{2}}=12v^{-4-1}(1)\\[5pt]
\frac{d^{2}f}{dz^{2}}=12(z+1)^{-5}
\end{gather}
\]
\[
\begin{gather}
f^{(2)}(z)=\frac{12}{(z+1)^{5}}
\end{gather}
\]
\[
\begin{gather}
\oint_{{|z-1|=1}}\frac{dz}{(z-1)^{3}(z+1)^{3}}=\frac{\cancel{2}\pi\mathrm{i}}{\cancel{2}.1}\;\frac{12}{(1+1)^{5}}\\[5pt]
\oint_{|z-1|=1}\frac{dz}{(z-1)^{3}(z+1)^{3}}=\pi\mathrm{i}\;\frac{12}{2^{5}}\\[5pt]
\oint_{|z-1|=1}\frac{dz}{(z-1)^{3}(z+1)^{3}}=\pi\mathrm{i}\;\frac{\cancelto{3}{12}}{\cancelto{8}{32}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\oint_{|z-1|=1}\frac{dz}{(z-1)^{3}(z+1)^{3}}=\;\frac{3\pi\mathrm{i}}{8}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .