Exercício Resolvido de Oscilações
publicidade
Um corpo de massa m se encontra apoiado sobre um suporte de madeira. O suporte começa a oscilar com um movimento harmônico simples, aumentando a frequência das oscilações até fazer com que o corpo comece a deslizar sobre a madeira.
a) Calcule o coeficiente de atrito entre o corpo e a madeira em função do período T e da amplitude A das oscilações;
b) Para o período T = 3 s e a amplitude A = 0,4 m qual é o coeficiente de atrito?
Dados do problema:
- Massa do corpo: m;
- Período das oscilações: T;
- Amplitude das oscilações: A.
As forças que atuam no sistema são a força peso
\( \vec{P} \),
a força de reação normal
\( \vec{N} \),
a força de atrito
\( {\vec{F}}_{at} \)
e a força externa
\( \vec{F} \)
(Figura 1).
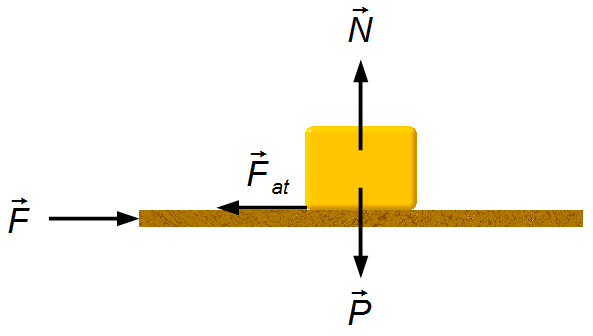
O sistema esta inicialmente em repouso em relação a uma posição O (Figura 2-A).
Uma força oscilante começa a atuar no suporte de madeira empurrando-o para frente e para trás. O corpo sobre o suporte permanece na mesma posição em relação ao suporte, mas não em relação à posição O, ele se desloca junto com o suporte (Figuras 2-B, 2-C e 2-D).
A força externa \( \vec{F} \) vai aumentando e enquanto ela for menor que a força de atrito \( {\vec{F}}_{at} \) o corpo permanece na mesma posição sobre o suporte (Figuras 2-B, 2-C e 2-D).
Essa situação continua até que a força externa seja maior que a força de atrito. Nesse momento o suporte se desloca por baixo do corpo e a força de atrito não é suficiente para fazer o corpo permanecer na mesma posição sobre o suporte (Figura 2-E).
Uma força oscilante começa a atuar no suporte de madeira empurrando-o para frente e para trás. O corpo sobre o suporte permanece na mesma posição em relação ao suporte, mas não em relação à posição O, ele se desloca junto com o suporte (Figuras 2-B, 2-C e 2-D).
A força externa \( \vec{F} \) vai aumentando e enquanto ela for menor que a força de atrito \( {\vec{F}}_{at} \) o corpo permanece na mesma posição sobre o suporte (Figuras 2-B, 2-C e 2-D).
Essa situação continua até que a força externa seja maior que a força de atrito. Nesse momento o suporte se desloca por baixo do corpo e a força de atrito não é suficiente para fazer o corpo permanecer na mesma posição sobre o suporte (Figura 2-E).

Solução
a) Aplicando a 2.ª Lei de Newton
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\vec{F}=m\vec{a}} \tag{I}
\end{gather}
\]
- Direção x:
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a=-\omega ^{2}A\cos \omega t}
\end{gather}
\]
a aceleração é máxima quando
\( \cos \omega t=1 \),
em módulo
\[
\begin{gather}
a_{max}=\omega ^{2}A \tag{II}
\end{gather}
\]
Substituindo a expressão (II) na expressão (I), a força externa máxima será
\[
\begin{gather}
F=m\omega ^{2}A \tag{III}
\end{gather}
\]
A frequência das oscilações é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\omega =\frac{2\pi}{T}} \tag{IV}
\end{gather}
\]
substituindo a expressão (IV) na expressão (III)
\[
\begin{gather}
F=mA\left(\frac{2\pi}{T}\right)^{2} \tag{V}
\end{gather}
\]
A força de atrito é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{at}=\mu N} \tag{VI}
\end{gather}
\]
- Direção y:
\[
\begin{gather}
P=N \tag{VII}
\end{gather}
\]
a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{VIII}
\end{gather}
\]
substituindo a expressão (VIII) na expressão (VII)
\[
\begin{gather}
N=mg \tag{IX}
\end{gather}
\]
Substituindo a expressão (IX) na expressão (VI)
\[
\begin{gather}
F_{at}=\mu mg \tag{X}
\end{gather}
\]
Igualando as expressões (V) e (X)
\[
\begin{gather}
\mu \cancel{m}g=\cancel{m}A\left(\frac{2\pi}{T}\right)^{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mu =\frac{A}{g}\left(\frac{2\pi}{T}\right)^{2}}
\end{gather}
\]
b) Para T = 3 s e A = 0,4 m, e adotando π =3,14 e g = 9,81 m/s2
\[
\begin{gather}
\mu =\frac{0,4}{9,81}.\left(\frac{2.3,14}{3}\right)^{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mu =0,1}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .