Exercício Resolvido de Momento de Inércia
publicidade
Um sistema é formado por três massas conectadas por barras de massas desprezívies, estãp localizadas nos
pontos indicados na figura.
a) Calcule a posição do Centro de Massa desse sistema;
b) Calcule o Momento de Inércia em relação ao Centro de Massa do sistema.
As massas e posições dos corpos são: mA = 5 kg, (xA, yA) = (8, 0), mB = 7 kg, (xB, yB) = (–4, 6) e mC = 2 kg, (xC, yC) = (1, –2).
a) Calcule a posição do Centro de Massa desse sistema;
b) Calcule o Momento de Inércia em relação ao Centro de Massa do sistema.
As massas e posições dos corpos são: mA = 5 kg, (xA, yA) = (8, 0), mB = 7 kg, (xB, yB) = (–4, 6) e mC = 2 kg, (xC, yC) = (1, –2).

Dados do problema:
- Massa do corpo A: mA = 5 kg;
- Posição do corpo A: (xA, yA) = (8, 0);
- Massa do corpo B: mB = 7 kg;
- Posição do corpo B: (xB, yB) = (–4, 6);
- Massa do corpo C: mC = 2 kg;
- Posição do corpo C: (xC, yC) = (1, –2).
Solução
a) O Centro de Massa é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{{\mathbf{r}}_{CM}=\frac{\displaystyle \sum_{i=1}^{n}m_{i}{\mathbf{r}}_{i}}{\displaystyle \sum_{i=1}^{n}m_{i}}}
\end{gather}
\]
O vetores posição dos corpos A, B e C são dados por (Figura 1)
\[
\begin{gather}
{\mathbf{r}}_{A}=8\;\mathbf{i}+0\;\mathbf{j}\\
{\mathbf{r}}_{A}=8\;\mathbf{i}
\end{gather}
\]
\[
\begin{gather}
{\mathbf{r}}_{B}=-4\;\mathbf{i}+6\;\mathbf{j}
\end{gather}
\]
\[
\begin{gather}
{\mathbf{r}}_{C}=1\;\mathbf{i}-2\;\mathbf{j}\\
{\mathbf{r}}_{C}=\mathbf{i}-2\;\mathbf{j}
\end{gather}
\]
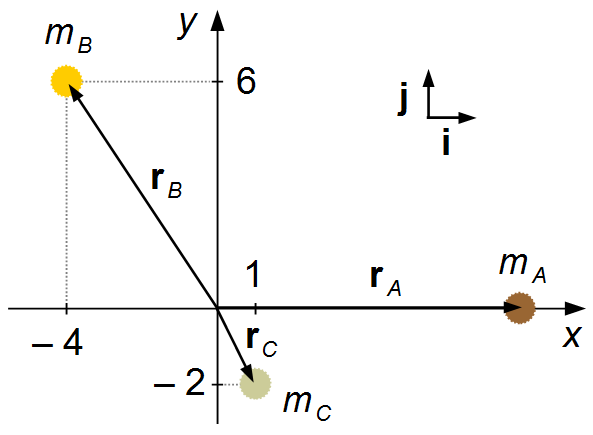
O vetor posição do Centro de Massa será
\[
\begin{gather}
{\mathbf{r}}_{CM}=\frac{\displaystyle \sum_{i=1}^{n}m_{i}x_{i}\;\mathbf{i}+\displaystyle \sum_{i=1}^{n}m_{i}y_{i}\;\mathbf{j}}{\displaystyle \sum_{i=1}^{n}m_{i}}\\[5pt]
{\mathbf{r}}_{CM}=\frac{(8.5+(-4).7+1.2)\;\mathbf{i}+(0.5+6.7+(-2).2)\;\mathbf{j}}{5+7+2}\\[5pt]
{\mathbf{r}}_{CM}=\frac{(40-28+2)\;\mathbf{i}+(0+42-4)\;\mathbf{j}}{14}\\[5pt]
{\mathbf{r}}_{CM}=\frac{14\;\mathbf{i}+38\;\mathbf{j}}{14}
\end{gather}
\]
Vetor posição do Centro de Massa (Figura 2)
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{{\mathbf{r}}_{CM}=\mathbf{i}+2,7\;\mathbf{j}}
\end{gather}
\]
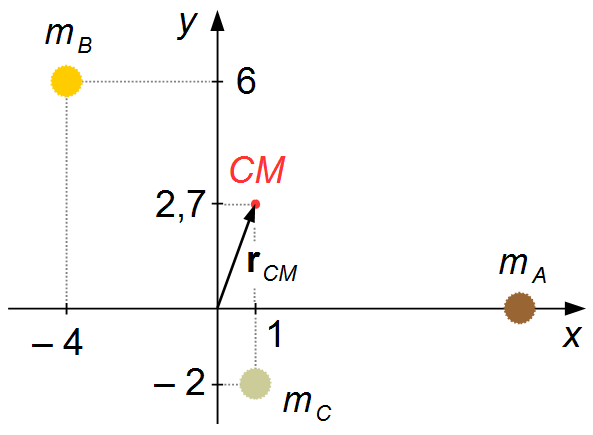
b) A distância r de cada corpo ao Centro de Massa será da pela fórmula da distância entre dois pontos (Figura 2)
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\left|\mathbf{r}\right|=r=\sqrt{\left(x-x_{CM}\right)^{2}+\left(y-y_{CM}\right)^{2}\;}}
\end{gather}
\]
A distância rA do corpo A ao Centro de Massa será (Figura 2)
\[
\begin{gather}
r_{A}=\sqrt{\left(x_{A}-x_{CM}\right)^{2}+\left(y_{A}-y_{CM}\right)^{2}\;}\\[5pt]
r_{A}=\sqrt{\left(8-1\right)^{2}+\left(0-2,7\right)^{2}\;}\\[5pt]
r_{A}=\sqrt{\left(7\right)^{2}+\left(-2,7\right)^{2}\;}\\[5pt]
r_{A}=\sqrt{49+7,3\;}\\[5pt]
r_{A}=\sqrt{56,3\;}\\[5pt]
r_{A}\approx 7,5
\end{gather}
\]
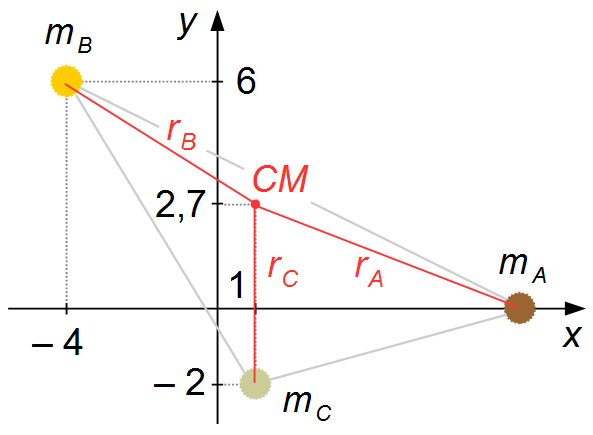
A distância rB do corpo B ao Centro de Massa será (Figura 2)
\[
\begin{gather}
r_{B}=\sqrt{\left(x_{B}-x_{CM}\right)^{2}+\left(y_{B}-y_{CM}\right)^{2}\;}\\[5pt]
r_{B}=\sqrt{\left(-4-1\right)^{2}+\left(6-2,7\right)^{2}\;}\\[5pt]
r_{B}=\sqrt{\left(-5\right)^{2}+\left(3,3\right)^{2}\;}\\[5pt]
r_{B}=\sqrt{25+10,9\;}\\[5pt]
r_{B}=\sqrt{35,9\;}\\[5pt]
r_{B}\approx 6
\end{gather}
\]
A distância rC do corpo C ao Centro de Massa será (Figura 2)
\[
\begin{gather}
r_{C}=\sqrt{\left(x_{C}-x_{CM}\right)^{2}+\left(y_{C}-y_{CM}\right)^{2}\;}\\[5pt]
r_{C}=\sqrt{\left(1-1\right)^{2}+\left(-2-2,7\right)^{2}\;}\\[5pt]
r_{C}=\sqrt{\left(0\right)^{2}+\left(-4,7\right)^{2}\;}\\[5pt]
r_{C}=\sqrt{22,1\;}\\[5pt]
r_{C}\approx 4,7
\end{gather}
\]
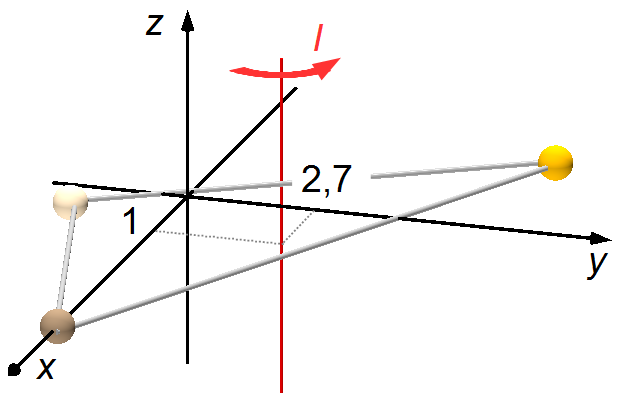
O Momento de Inércia em relação ao eixo que passa pelo Centro de Massa é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I_{CM}=\sum_{i=1}^{n}m_{i}r_{i}^{2}}
\end{gather}
\]
substituindo as distâncias rA, rB e rC obtidas
acima (Figura 3)
\[
\begin{gather}
I=5.(7,5)^{2}+7.(6)^{2}+2.(4,7)^{2}\\[5pt]
I=5.56,3+7.36+2.22,1\\[5pt]
I=281,5+252+44,2
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{I=577,7 \;\text{kg.m}^{2}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .