Exercício Resolvido de Momento de Inércia
publicidade
Um sistema é formado por quatro corpos pontuais conectados por barras de massa desprezível, localizados
nos vértices de uma quadrado de lado R. Calcule o momento de inércia em relação a um eixo que
passa pelo centro do quadrado e perpendicular ao plano que contém as massas nos seguintes casos:
a) Os quatro corpos têm massas iguais a M;
b) Os corpos têm massas iguais a 1 kg, 2 kg, 3kg, 4 kg e R = 2 m.
a) Os quatro corpos têm massas iguais a M;
b) Os corpos têm massas iguais a 1 kg, 2 kg, 3kg, 4 kg e R = 2 m.

Dados do problema:
- Distância entre os corpos: R.
a) A distância r de um dos corpos ao centro será a metade da diagonal d do quadrado de lado R. Aplicando o Teorema de Pitágoras (Figura 1)
\[
\begin{gather}
d^{2}=R^{2}+R^{2}\\
d^{2}=2R^{2}\\
d=\sqrt{2R^{2}\;}\\
d=R\sqrt{2\;}
\end{gather}
\]
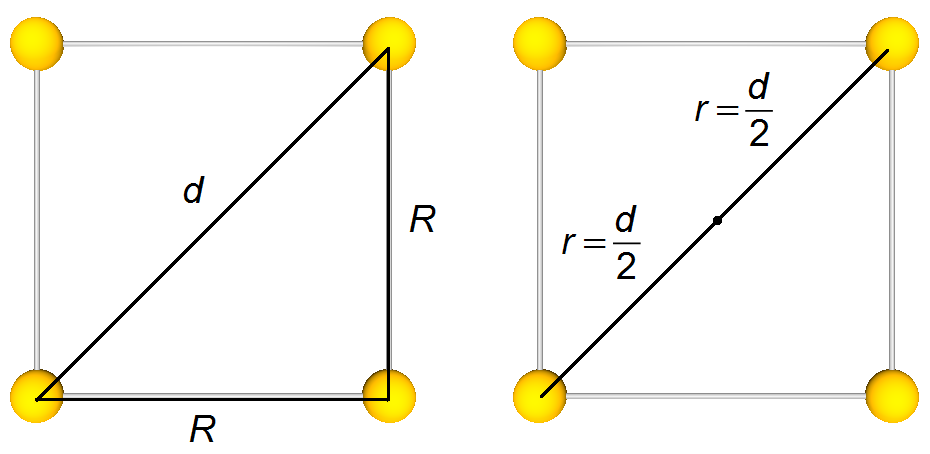
\[
\begin{gather}
r=\frac{R\sqrt{2\;}}{2} \tag{I}
\end{gather}
\]
O momento de inércia em relação ao eixo é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I=\sum _{i=1}^{n}m_{i}r_{i}^{2}} \tag{II}
\end{gather}
\]
como todos os corpos têm a mesma massa e estão a mesma distância do centro
\[
\begin{gather}
I=M\left(\frac{R\sqrt{2}\;}{2}\right)^{2}+M\left(\frac{R\sqrt{2}\;}{2}\right)^{2}+M\left(\frac{R\sqrt{2}\;}{2}\right)^{2}+M\left(\frac{R\sqrt{2}\;}{2}\right)^{2}\\
I=4M\frac{R^{2}2}{4}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{I=2MR^{2}}
\]
b) Substituindo as massas dadas e a distância ao eixo dada pela expressão (I) na expressão (II)
\[
\begin{gather}
I=1.\left(\frac{2\sqrt{2}\;}{2}\right)^{2}+2.\left(\frac{2\sqrt{2}\;}{2}\right)^{2}+3.\left(\frac{2\sqrt{2}\;}{2}\right)^{2}+4.\left(\frac{2\sqrt{2}\;}{2}\right)^{2}\\
I=1.2+2.2+3.2+4.2\\
I=2+4+6+8
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{I=20\;\text{kg.m}^{2}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .