Exercício Resolvido de Momento de Inércia
publicidade
Um sistema é formado por dois corpos de massas M e m (M>m) conectados uma
barra de massa desprezível, a dustância entre os centros dos corpos é igual a R. Calcule o momento
de inércia em relação a um eixo que passa pelo centro de massa do sistema.

Dados do problema:
- Massa do corpo 1: M;
- Massa do corpo 2: m;
- Distância entre os corpos: R.
Em primeiro lugar devemos determinar a posição do centro de massa do sistema para sabermos a distância
de cada corpo até o centro de massa. Vamos adotar um sistema de referência com origem no corpo de massa
M e orientado para a direita (Figura 1).
O corpo de massa M está na origem do referencial, r1 = 0, o centro de massa está a uma distância rCM da origem e o corpo de massa m a uma distância r2 = R.
A posição do Centro de Massa é dada por
O corpo de massa M está na origem do referencial, r1 = 0, o centro de massa está a uma distância rCM da origem e o corpo de massa m a uma distância r2 = R.
A posição do Centro de Massa é dada por

Figura 1
\[ \bbox[#99CCFF,10px]
{r_{CM}=\frac{\sum_{i=1}^{n}m_{i}{\mathbf{r}}_{i}}{\sum_{i=1}^{n}m_{i}}}
\]
para n = 2
\[
\begin{gather}
r_{CM}=\frac{m_{1}r_{1}+m_{2}r_{2}}{m_{1}+m_{2}}\\
r_{CM}=\frac{M.0+mR}{M+m}\\r_{CM}=\frac{mR}{M+m} \tag{I}
\end{gather}
\]
O corpo 1 está a uma distância r1 = rCM do eixo que passa pelo
centro de massa, e o corpo 2 está a uma distância
r2 = R−r1 do eixo (Figura 2).
Observação: Não confundir o r1 no cálculo da posição do centro de
massa, que representava a distância do corpo 1 à origem do sistema de referência,
r1 = 0, na primeira parte do problema, com r1 usado aqui para
representar a distância do corpo 1 ao eixo que passa pelo centro de massa,
r1 = rCM.
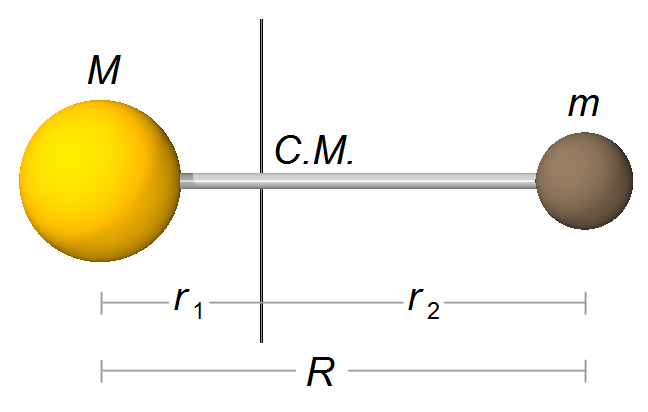
Figura 2
O momento de inércia em relação ao eixo é dado por
\[ \bbox[#99CCFF,10px]
{I=\sum_{i=1}^{n}m_{i}r_{i}^{2}}
\]
para n =2, e substituindo r1 pela expressão (I)
\[
\begin{gather}
I=m_{1}r_{1}^{2}+m_{1}r_{1}^{2}\\[5pt]
I=M\left(\frac{mR}{M+m}\right)^{2}+m(R-r_{1})^{2}\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+m\left(R-\frac{mR}{M+m}\right)^{2}\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+m\left[R\left(1-\frac{m}{M+m}\right)\right]^{2}\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+mR^{2}\left(1-\frac{m}{M+m}\right)^{2}\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+mR^{2}\left(\frac{M+m-m}{M+m}\right)^{2}\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+mR^{2}\left(\frac{M^{2}}{\left(M+m\right)^{2}}\right)\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+mR^{2}\left(\frac{M^{2}}{\left(M+m\right)^{2}}\right)\\[5pt]
I=\frac{Mm^{2}R^{2}}{\left(M+m\right)^{2}}+\frac{M^{2}mR^{2}}{\left(M+m\right)^{2}}\\[5pt]
I=\frac{Mm}{\left(M+m\right)^{2}}R^{2}+\left(M+m\right)\\[5pt]
I=\frac{Mm}{M+m}R^{2}
\end{gather}
\]
fazendo a seguinte definição
\( \mu =\frac{Mm}{M+m} \)
\[ \bbox[#FFCCCC,10px]
{I=\mu R^{2}}
\]
Observação: μ é chamado de massa reduzida, o problema de dois corpos passa a ser o
problema de um único corpo girando em torno de um ponto fixo. A massa reduzida e é usada em vários campos
da física.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .