Exercício Resolvido de Cinemática

Um móvel está sobre um plano-xy, inicialmente em repouso na posição x₀ sobre o eixo-x positivo. Ele começa a se movimentar com velocidades constantes v_x, no sentido da origem, e v_y no sentido do eixo-y positivo. Determinar depois de quanto tempo este móvel se encontrará a distância mínima da origem e, qual é essa distância mínima.

Dados do problema:

Posição inicial do móvel: x₀;
Velocidade do móvel na direção x: v_x;
Velocidade do móvel na direção y: v_y.

Esquema do problema:

Como as componentes da velocidade são constantes a trajetória será uma reta (Figura 1-A).

Figura 1

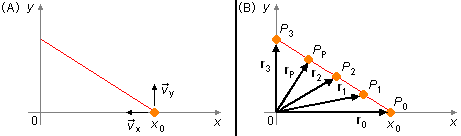
Ao longo da trajetória o móvel passa sucessivamente pelos pontos P₀, P₁, P₂, P_P, P₃ e assim por diante, localizados pelos vetores posição r₀, r₁, r₂, r_P, r₃, respectivamente. O ponto de menor distância à origem será o ponto P_P onde o vetor r_P é perpendicular a um vetor da trajetória (Figura 1-B).

Solução

O vetor posição r_P é escrito como

\[ \begin{gather} {\mathbf{r}}_{P}={\mathbf{r}}_{0}+\mathbf{v} t \tag{I} \end{gather} \]

que é a equação vetorial para o Movimento Retilíneo Uniforme (M.R.U.), o vetor posição inicial r₀ só possui componente ao longo da direção x, \( {\mathbf{r}}_{0}={x}_{0}\;\mathbf{i} \), o vetor ao longo da trajetória possui componentes nas direções x e y, \( \mathbf{v}\;t=-v_{x}t\;\mathbf{i}+v_{y}t\;\mathbf{j} \) (Figura 2-A), assim a expressão (I) pode ser escrita como

\[ \begin{gather} {\mathbf{r}}_{P}={x}_{0}\;\mathbf{i}+\left(-{v}_{x}t\;\mathbf{i}+{v}_{y}t\;\mathbf{j}\right)\\ {\mathbf{r}}_{P}={x}_{0}\;\mathbf{i}-{v}_{x}t\;\mathbf{i}+{v}_{y}t\;\mathbf{j}\\ {\mathbf{r}}_{P}=\left({x}_{0}-{v}_{x}t\right)\;\mathbf{i}+{v}_{y}t\;\mathbf{j} \tag{II} \end{gather} \]

Figura 2

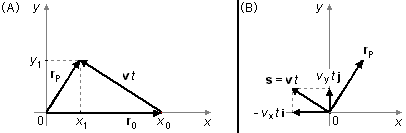
O vetor deslocamento \( \mathbf{s}=-v_{x}t\;\mathbf{i}+v_{y}t\;\mathbf{j} \) é paralelo a trajetória (Figura 2-B), para que os vetores r_P e s sejam perpendiculares entre si devemos ter a condição de que o Produto Escalar entre eles seja nulo

\[ \begin{gather} {\mathbf{r}}_{P}\cdot{\mathbf{s}}=0\\[5pt] \left[\left(x_{0}-v_{x}t\right)\;\mathbf{i}+v_{y}t\;\mathbf{j}\right]\cdot\left[-v_{x}t\;\mathbf{i}+v_{y}t\;\mathbf{j}\right]=0\\[5pt] \left(x_{0}-v_{x}t\right)\left(-v_{x}t\right)\underbrace{\mathbf{i}\cdot\mathbf{i}}_{1}+v_{y}t\;v_{y}t\underbrace{\mathbf{j}\cdot\mathbf{j}}_{1}=0\\[5pt] -x_{0}v_{x}t+v_{x}^{2}t^{2}+v_{y}^{2}t^{2}=0\\[5pt] t\left(-x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t\right)=0 \end{gather} \]

desta expressão temos dois valores para o tempo

\[ \begin{gather} t=0\\[5pt] \text{ou}\\[5pt] -x_{0}v_{x}+v_{x}^{2}t+v_{y}^{2}t=0\\ t\left(v_{x}^{2}+v_{y}^{2}\right)=x_{0}v_{x} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {t=\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}} \]

Substituindo este valor na expressão (II) temos o vetor posição que dá a distância mínima do móvel à origem

\[ {\mathbf{r}}_{P}=\left({x}_{0}-{v}_{x}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)\;\mathbf{i}+{v}_{y}t\;\mathbf{j} \]

que tem como módulo

\[ \begin{gather} r_{P}=\sqrt{\left(x_{0}-v_{x}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(v_{y}\frac{x_{0}v_{x}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt] r_{P}=\sqrt{\left(\frac{x_{0}(v_{x}^{2}+v_{y}^{2})-x_{0}v_{x}^{2}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(\frac{x_{0}v_{x}v_{y}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt] r_{P}=\sqrt{\;\left(\frac{{x}_{0}v_{y}^{2}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}+\left(\frac{x_{0}v_{x}{v}_{y}}{v_{x}^{2}+v_{y}^{2}}\right)^{2}\;}\\[5pt] r_{P}=\sqrt{\frac{{x}_{0}^{2}v_{y}^{4}+x_{0}^{2}v_{x}^{2}v_{y}^{2}}{(v_{x}^{2}+v_{y}^{2})^{2}}\;}\\[5pt] r_{P}=\sqrt{\frac{{x}_{0}^{2}v_{y}^{2}(v_{y}^{2}+v_{y}^{2})}{(v_{x}^{2}+v_{y}^{2})^{2}}\;}\\[5pt] r_{P}=\sqrt{\frac{{x}_{0}^{2}v_{y}^{2}}{v_{x}^{2}+v_{y}^{2}}\;} \end{gather} \]

\[ \bbox[#FFCCCC,10px] {r_{P}=\frac{{x}_{0}v_{y}}{\sqrt{v_{x}^{2}+v_{y}^{2}\;}}} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .