Exercício Resolvido de Cinemática
publicidade
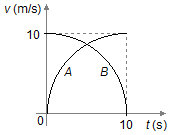
O móvel B parte do ponto O no mesmo instante em que por esse ponto passa o móvel A.
Ambos os móveis percorrem a mesma trajetória retilínea e as curvas velocidade×tempo são quartos de
circunferência com raios iguais, como mostra a figura. Determinar:
a) O instante em os móveis possuem velocidades iguais em módulo;
b) O valor desta velocidade;
c) O instante em os móveis possuem acelerações iguais em módulo;
d) O valor desta aceleração.
a) O instante em os móveis possuem velocidades iguais em módulo;
b) O valor desta velocidade;
c) O instante em os móveis possuem acelerações iguais em módulo;
d) O valor desta aceleração.
Solução
A equação de uma circunferência é dada por
\[ \bbox[#99CCFF,10px]
{(x-x_{0})^{2}+(y-y_{0})^{2}=r^{2}}
\]
onde x0 e y0 são as coordenadas do centro da circunferência e r o
seu raio.Como o gráfico das velocidades em função do tempo são arcos de circunferência, podemos fazer as seguintes associações x = t, y = v e r = 10.
Para o móvel B temos uma circunferência centrada na origem
(x0, y0) = (0, 0) (Figura 1), assim a equação da velocidade será
\[
\begin{gather}
t^{2}+v_{B}^{2}=10^{2}\\
v_{B}^{2}=100-t^{2} \tag{I}\\
v_{B}=\sqrt{100-t^{2}\;} \tag{I}
\end{gather}
\]
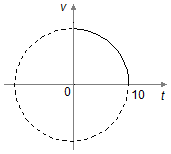
Figura 1
Para o móvel A temos uma circunferência centrada em
(x0, y0) = (10, 0) (Figura 2), assim a equação da velocidade será
\[
\begin{gather}
(t-10)^{2}+v_{A}^{2}=10^{2}\\
v_{A}^{2}=100-(t-10)^{2} \tag{III}\\
v_{A}=\sqrt{100-(t-10)^{2}\;} \tag{IV}
\end{gather}
\]
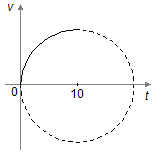
Figura 2
a) Impondo a condição de que as velocidades são iguais e usando as expressões (I) e (III)
\[
\begin{gather}
v_{B}^{2}=v_{A}^{2}\\
100-t^{2}=100-(t-10)^{2}\\
t^{2}=(t-10)^{2}\\
t^{2}=t^{2}-20t+100\\
-20t-100=0\\
t=\frac{100}{20}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=5\;\text{s}}
\]
b) Substituindo o resultado do item anterior na expressão (II)
\[
\begin{gather}
v_{B}=\sqrt{100-5^{2}\;}\\
v_{B}=\sqrt{75\;}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{v_{A}=v_{B}=8,7\;\text{m/s}}
\]
c) A aceleração é dada por
\[ \bbox[#99CCFF,10px]
{a=\frac{dv}{dt}}
\]
derivando as expressões (II) e (IV) em relação ao tempo temos as acelerações aA e
aB dos móveis.
Derivada de \( v_{B}=\sqrt{100-t^{2}\;} \)
a função vB(t) é uma função composta cuja derivada é dada pela regra da cadeia
a função vB(t) é uma função composta cuja derivada é dada pela regra da cadeia
\[
\begin{gather}
\frac{dv[u(t)]}{dt}=\frac{dv}{du}\frac{du}{dt} \tag{V}
\end{gather}
\]
com
\( v(u)=\sqrt{u\;} \)
e
\( u(t)=100-t^{2} \),
assim as derivadas serão
\[
\begin{gather}
\frac{dv}{du}=u^{\frac{1}{2}}=\frac{1}{2}u^{\frac{1}{2}-1}=\frac{1}{2}u^{-{\frac{1}{2}}}=\frac{1}{2\sqrt{u\;}} \tag{VI}
\end{gather}
\]
\[
\begin{gather}
\frac{du}{dt}=-2t \tag{VII}
\end{gather}
\]
substituindo as expressões (VI) e (VII) na expressão (V)
\[
\frac{dv_{B}}{dt}=\frac{1}{2\sqrt{u\;}}(-2t)=\frac{-{t}}{\sqrt{100-t^{2}\;}}
\]
\[
\begin{gather}
a_{B}=-{\frac{t}{\sqrt{100-t^{2}\;}}} \tag{VIII}
\end{gather}
\]
Derivada de \( v_{A}=\sqrt{100-(t-10)^{2}\;} \)
a função vA(t) é uma função composta cuja derivada é dada pela regra da cadeia
a função vA(t) é uma função composta cuja derivada é dada pela regra da cadeia
\[
\begin{gather}
\frac{dv[u(t)]}{dt}=\frac{dv}{du}\frac{du}{dt} \tag{IX}
\end{gather}
\]
com
\( v(u)=\sqrt{u\;} \)
e
\( u(t)=100-(t-10)^{2} \),
assim as derivadas serão
\[
\begin{gather}
\frac{dv}{du}=u^{\frac{1}{2}}=\frac{1}{2}u^{\frac{1}{2}-1}=\frac{1}{2}u^{-{\frac{1}{2}}}=\frac{1}{2\sqrt{u\;}} \tag{X}
\end{gather}
\]
\[
\begin{gather}
\frac{du}{dt}=-2(t-10) \tag{XI}
\end{gather}
\]
substituindo as expressões (X) e (XI) na expressão (IX)
\[
\frac{dv_{A}}{dt}=\frac{1}{2\sqrt{u\;}}[-2(t-10)]=\frac{-(t-10)}{\sqrt{100-(t-10)^{2}}}
\]
\[
\begin{gather}
a_{A}=-{\frac{t-10}{\sqrt{100-(t-10)^{2}}}} \tag{XII}
\end{gather}
\]
Impondo a condição de que as acelerações são iguais e usando as expressões (VIII) e (XII)
\[
\begin{gather}
a_{B}=a_{A}\\[5pt]
-{\frac{t}{\sqrt{100-t^{2}}}}=-{\frac{t-10}{\sqrt{100-(t-10)^{2}}}}\\[5pt]
\left[-{\frac{t}{\sqrt{100-t^{2}}}}\right]^{2}=\left[-{\frac{t-10}{\sqrt{100-(t-10)^{2}}}}\right]^{2}\\[5pt]
\frac{t^{2}}{100-t^{2}}=\frac{(t-10)^{2}}{100-(t-10\;)^{2}\;}\\[5pt]
t^{2}\left[100-(t-10\;)^{2}\right]=(t-10)^{2}(100-t^{2})\\[5pt]
100t^{2}-\cancel{[t^{2}(t-10)^{2}]}=100(t-10)^{2}-\cancel{[t^{2}(t-10)^{2}]}\\[5pt]
100t^{2}=100(t-10)^{2}\\[5pt]
t^{2}=t^{2}-20t+100\\[5pt]
-20t+100=0\\[5pt]
t=\frac{100}{20}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{t=5\;\text{s}}
\]
d) Substituindo o resultado do item anterior na expressão (VIII)
\[
\begin{gather}
a_{B}=-\frac{{5}}{\sqrt{100-5^{2}\;}}\\
a_{B}=-\frac{{5}}{\sqrt{100-25\;}}\\
a_{B}=-\frac{{5}}{\sqrt{75\;}}\\
a_{B}=-\frac{{5}}{8,7}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{B}\simeq -0,6\;\text{m/s}^{2}}
\]
Substituindo o resultado do item anterior na expressão (XIII)
\[
\begin{gather}
a_{A}=-\frac{{5-10}}{\sqrt{100-(5-10)^{2}\;}}\\
a_{A}=-\frac{{-5}}{\sqrt{100-(-5)^{2}\;}}\\
a_{A}=\frac{5}{\sqrt{100-25\;}}\\
a_{A}=\frac{5}{\sqrt{75\;}}\\
a_{B}=\frac{-{5}}{8,7}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{a_{A}\simeq 0,6\;\text{m/s}^{2}}
\]
Observação: Vemos que em módulo as acelerações dos móveis são iguais (0,6 m/s2), mas
elas possuem sinais contrários, enquanto o móvel B está diminuindo sua velocidade (freando), o móvel
A está aumentando a velocidade (acelerando), o que concorda com as curvas mostradas no gráfico do problema.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .