Exercício Resolvido de Cinemática
publicidade
Determinar o vetor aceleração de um corpo que desliza, a partir do repouso por uma canaleta disposta de
forma helicoidal com passo k e raio R ao final da n-ésima volta, despreza-se o
atrito.
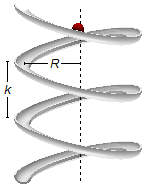
Dados do problema:
- Velocidade inicial do corpo: v0 = 0,
- Raio do helicoide: R;
- Passo do helicoide: k.
Adotamos um sistema de referência cilíndrico (Figura 1-A) onde \( {\mathbf{e}}_{r} \), \( {\mathbf{e}}_{z} \) e \( {\mathbf{e}}_{\theta } \) são os vetores unitários das direções r, z e θ.
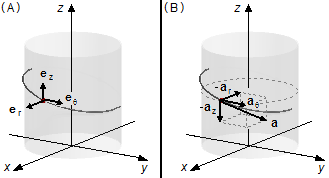
O vetor aceleração a do corpo aponta para o centro do helicoide na descendente. Este vetor pode ser decomposto em três componentes (Figura 1-B), na direção z a componente \( -{\mathbf{a}}_{z} \) apontando para baixo, na direção r a componente \( -{\mathbf{a}}_{r} \) apontando para o centro da curva e na direção θ a componente \( {\mathbf{a}}_{\theta } \) a tangente à curva.
Solução
O vetor aceleração é dado por
\[
\begin{gather}
\mathbf{a}=-a_{r}{\mathbf{e}}_{r}+a_{\theta}{\mathbf{e}}_{\theta}-a_{z}{\mathbf{e}}_{z} \tag{I}
\end{gather}
\]
O módulo da componente na direção r representa a aceleração centrípeta do corpo dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{a_{r}=\frac{v^{2}}{r}} \tag{II}
\end{gather}
\]
Desenrolando uma volta do helicoide, o passo k representa o cateto de um triângulo retângulo, a projeção do
helicoide num plano é uma circunferência de raio R, que desenrolada tem um comprimento 2πR,
formando outro cateto (Figura 2). Pelo Teorema de Pitágoras a hipotenusa será
\[
\begin{gather}
h^{2}=k^{2}+(2\pi R)^{2}\\
h=\sqrt{k^{2}+4\pi^{2}R^{2}\;} \tag{III}
\end{gather}
\]
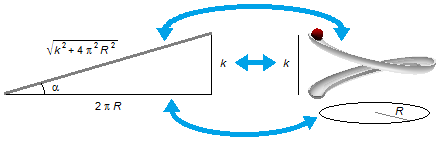
que representa o comprimento de uma volta do helicoide.
Da Figura 2 temos as seguintes relações
\[
\begin{gather}
\cos \alpha =\frac{2\pi R}{\sqrt{k^{2}+4\pi^{2}R^{2}\;}} \tag{IV-a}
\end{gather}
\]
\[
\begin{gather}
\operatorname{sen}\alpha =\frac{k}{\sqrt{k^{2}+4\pi^{2}R^{2}\;}} \tag{IV-b}
\end{gather}
\]
A velocidade do corpo é tangente a trajetória helicoidal (Figura 3-A), decompondo a velocidade nas direções
θ e z temos as componentes vθ e vz. O ângulo entre o
vetor velocidade paralelo ao plano inclinado vT e a direção θ é α, o
mesmo ângulo de inclinação do plano, estes ângulos são alternos internos (Figura 3-B).
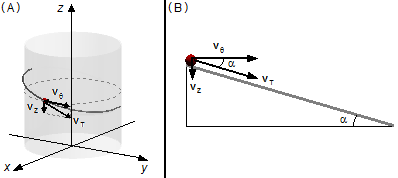
A componente vθ é tangente à curva esta componente é usada para o cálculo da aceleração centrípeta dada pela expressão (II)
\[
v_{\theta }=v_{T}\cos \alpha
\]
substituindo v = vθ e r = R em (II)
\[
\begin{gather}
a_{r}=\frac{v_{\theta }^{2}}{R}\\
a_{r}=\frac{(v_{T}\cos\theta )^{2}}{R}\\
a_{r}=\frac{v_{T}^{2}\cos ^{2}\theta}{R}
\end{gather}
\]
usando o valor do cosseno obtido em (IV)
\[
\begin{gather}
a_{r}=\frac{v_{T}^{2}}{R}\left(\frac{2\pi R}{\sqrt{k^{2}+4\pi^{2}R^{2}\;}}\right)^{2}\\
a_{r}=\frac{v_{T}^{2}}{R}\frac{4\pi^{2}R^{2}}{k^{2}+4\pi ^{2}R^{2}}\\
a_{r}=v_{T}^{2}\frac{4\pi^{2}R}{k^{2}+4\pi ^{2}R^{2}} \tag{V}
\end{gather}
\]
O módulo da velocidade tangencial vT é encontrado usando o
Princípio da Conservação da Energia Mecânica. Desenroladas todas as n voltas do helicoide
teremos um plano inclinado de altura n.k. A energia mecânica inicial
(\( E_{M}^{i} \))
no topo do plano, é igual à energia mecânica final
(\( E_{M}^{f} \)), na base do plano (Figura 4).
\[
E_{M}^{i}=E_{M}^{f}
\]
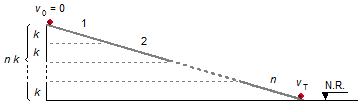
Adotando o Nível de Referência (N.R.) na base do plano inclinado e a aceleração da gravidade como g. Temos que, no topo do plano só há energia potencial devido à altura, a energia cinética é nula, v0 = 0, na base do plano só há energia cinética, a energia potencial é nula, H = 0.
A Energia Potencial é dada por
\[ \bbox[#99CCFF,10px]
{E_{P}=mgH}
\]
A Energia Cinética é dada por
\[ \bbox[#99CCFF,10px]
{E_{C}=\frac{mv^{2}}{2}}
\]
\[
\begin{gather}
E_{P}^{i}=E_{C}^{f}\\
mgH=\frac{mv^{2}}{2}\\
mgnk=\frac{mv_{T}^{2}}{2}\\
gnk=\frac{v_{T}^{2}}{2}\\
v_{T}^{2}=gnk \tag{VI}
\end{gather}
\]
substituindo a expressão (VI) em (V) a componente na direção r será
\[
\begin{gather}
a_{r}=2gnk\frac{4\pi ^{2}R}{k^{2}+4\pi^{2}R^{2}}\\
a_{r}=\frac{8\pi ^{2}Rgnk}{k^{2}+4\pi^{2}R^{2}} \tag{VII}
\end{gather}
\]
A aceleração da gravidade aponta verticalmente para baixo, a projeção da aceleração da gravidade na direção do plano
inclinado será g sen α (Figura 5-A)
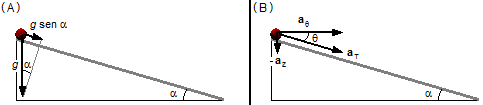
Na expressão (I) os termos da aceleração nas direções z e θ representam o vetor aceleração tangente à trajetória aT. Este vetor coincide com a componente da aceleração da gravidade na direção do plano inclinado (Figura 5-B)
\[
a_{T}=g\operatorname{sen}\alpha
\]
Observação: O vetor aceleração aT é tangente à trajetória em cada
ponto do helicoide,
\( {\mathbf{a}}_{T}=a_{T}{\mathbf{e}}_{T} \),
onde eT é o vetor unitário que dá a direção do vetor aceleração,
\( {\mathbf{e}}_{T}=\dfrac{{\mathbf{a}}_{T}}{a_{T}} \).
O vetor aceleração pode ser escrito em termos dos vetores unitários ez e eθ como sendo \( {\mathbf{a}}_{T}=a_{\theta }{\mathbf{e}}_{\theta}-a_{z}{\mathbf{e}}_{z} \)
O vetor aceleração pode ser escrito em termos dos vetores unitários ez e eθ como sendo \( {\mathbf{a}}_{T}=a_{\theta }{\mathbf{e}}_{\theta}-a_{z}{\mathbf{e}}_{z} \)
\[
{\mathbf{e}_{T}=\frac{a_{\theta}{\mathbf{e}}_{\theta}-a_{z}{\mathbf{e}}_{z}}{a_{T}}}
\]
Usando a expressão para o seno obtido em (IV)
\[
\begin{gather}
a_{T}=g\frac{k}{\sqrt{k^{2}+4\pi ^{2}R^{2}\;}} \tag{VIII}
\end{gather}
\]
O vetor aceleração tangente à trajetória pode ser escrito em termos das componentes nas direções z
e θ
\[
{\mathbf{a}}_{T}=a_{\theta}{\mathbf{e}}_{\theta}-a_{z}{\mathbf{e}}_{z}
\]
e a expressão (I) pode ser reescrita como
\[
\begin{gather}
\mathbf{a}=-a_{r}{\mathbf{e}}_{r}+a_{T}{\mathbf{e}}_{T} \tag{IX}
\end{gather}
\]
substituindo as expressões (VII) e (VIII) na expressão (IX)
\[
\mathbf{a}=-{\frac{8\pi^{2}Rgnk}{k^{2}+4\pi^{2}R^{2}}}{\mathbf{e}}_{r}+\frac{gk}{\sqrt{k^{2}+4\pi^{2}R^{2}\;}}{\mathbf{e}}_{T}
\]
colocando o temo
\( \dfrac{gk}{\sqrt{k^{2}+4\pi ^{2}R^{2}\;}} \)
em evidência
\[ \bbox[#FFCCCC,10px]
{\mathbf{a}=\frac{gk}{\sqrt{k^{2}+4\pi^{2}R^{2}\;}}\left(\frac{-{8\pi ^{2}Rn}}{\sqrt{\;k^{2}+4\pi^{2}R^{2}\;}}{\mathbf{e}}_{r}+{\mathbf{e}}_{T}\right)}
\]
e seu módulo será
\[
a=\frac{gk}{\sqrt{\;k^{2}+4\pi ^{2}R^{2}\;}}\left[\left(\frac{-{8\pi^{2}Rn}}{\sqrt{k^{2}+4\pi^{2}R^{2}\;}}\right)^{2}+1^{2}\right]^{1/2}
\]
\[ \bbox[#FFCCCC,10px]
{a=\frac{gk}{\sqrt{k^{2}+4\pi ^{2}R^{2}\;}}\left[\frac{64\pi^{4}R^{2}n^{2}}{k^{2}+4\pi ^{2}R^{2}\;}+1\right]^{1/2}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .