Exercício Resolvido de Lei de Gauss
publicidade
Determine o módulo do campo elétrico de um fio infinito carregado com uma distribuição de cargas de densidade linear constante λ.
Dados do problema:
- Densidade linear de cargas: λ.
Vamos assumir que o fio está carregado com uma carga positiva (Q > 0) e seu raio é desprezível.
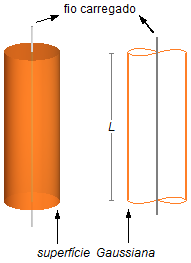
Para determinar o módulo do campo elétrico devemos considerar apenas os pontos no exterior do fio (como desprezamos o raio do fio não consideramos pontos internos), envolvendo o fio infinito por uma superfície Gaussiana de comprimento L (Figura 1).
Para determinar o módulo do campo elétrico devemos considerar apenas os pontos no exterior do fio (como desprezamos o raio do fio não consideramos pontos internos), envolvendo o fio infinito por uma superfície Gaussiana de comprimento L (Figura 1).
Solução
A Lei de Gauss no diz que
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\oint_{A}{\mathbf{E}}.d\mathbf{A}=\frac{q}{\epsilon_{0}}} \tag{I}
\end{gather}
\]
O campo elétrico se espalha radialmente a partir da distribuição de cargas na direção
er, e em cada elemento de área dA da superfície temos um vetor unitário
n perpendicular à superfície e orientado para fora (Figura 2).
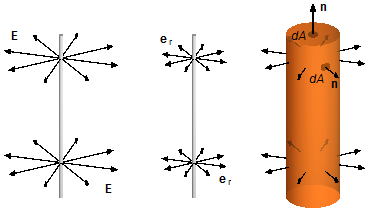
O vetor campo elétrico só possui componente na direção er pode ser escrito como
\[
\begin{gather}
\mathbf{E}=E{\;\mathbf{e}}_{r} \tag{II}
\end{gather}
\]
O vetor elemento de área pode ser escrito como
\[
\begin{gather}
d\mathbf{A}=dA\;\mathbf{n} \tag{III}
\end{gather}
\]
substituindo as expressões (II) e (III) na expressão (I)
\[
\oint_{A}E\;{\mathbf{e}}_{r}.dA\;\mathbf{n}=\frac{q}{\epsilon_{0}}
\]
Nas partes superior e inferior da superfície Gaussiana o vetor campo elétrico e o vetor elemento
de área são ortogonais (Figura 3)
\[
\oint_{A}E\;dA\;\underbrace{{\mathbf{e}}_{r}.\mathbf{n}}_{0}=\frac{q}{\epsilon_{0}}
\]
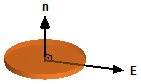
Figura 3
Observação: Como er e n são vetores unitários seus módulos
são iguais a 1 e como ambos estão em direções perpendiculares entre si o ângulo entre eles é
\( \theta =\frac{\pi}{2} \)
\( \mathbf{e}_{r}.\mathbf{n}=|\;\mathbf{e}_{r}\;|\;|\;\mathbf{n}\;|\;\cos\frac{\pi}{2}=1.1.0=0 \)
\[ \mathbf{e}_{r}.\mathbf{n}=|\;\mathbf{e}_{r}\;|\;|\;\mathbf{n}\;|\;\cos\frac{\pi}{2}=1.1.0=0 \]
.
Então o fluxo do campo elétrico nesta direção é nulo \( \Phi_{\text{E}}={\large\oint}_{A}E\;d A .0=0 \) e não contribui para o campo elétrico do fio.
Na lateral da superfície Gaussiana
\[
\oint_{A}E\;dA\;\underbrace{{\mathbf{e}}_{r}.\mathbf{n}}_{1}=\frac{q}{\epsilon_{0}}
\]
Observação: Como er e n são vetores unitários seus módulos são
iguais a 1 e como ambos estão na mesma direção e sentido o ângulo entre eles é nulo (θ = 0)
\( {\mathbf{e}}_{r}.\mathbf{n}=|\;{\mathbf{e}}_{r}\;|\;|\;\mathbf{n}\;|\;\cos 0=1.1.1=1 \)
\[ {\mathbf{e}}_{r}.\mathbf{n}=|\;{\mathbf{e}}_{r}\;|\;|\;\mathbf{n}\;|\;\cos 0=1.1.1=1 \]
.
\[
\begin{gather}
\oint_{A}E\;dA=\frac{q}{\epsilon_{0}} \tag{IV}
\end{gather}
\]
O elemento de área dA em coordenadas cilíndricas será (Figura 4-A)
\[
\begin{gather}
dA=r\;d\phi \;dz \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (VI)
\[
\begin{gather}
\int_{A}E\;r\;d\phi \;dz=\frac{q}{\epsilon_{0}} \tag{VI}
\end{gather}
\]
Como o campo elétrico é uniforme e a integral não depende do raio, o campo pode “sair” da integral e como não
existem termos “cruzados” em z e ϕ as integrais podem ser separadas
\[
Er\int d\phi \int dz=\frac{q}{\epsilon_{0}}
\]
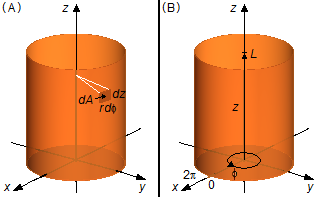
Os limites de integração serão de 0 a L em dz de 0 e 2π em dϕ, uma volta completa no cilindro (Figura 4-B)
\[
Er\int_{0}^{{2\pi}}d\phi \int_{0}^{L}dz=\frac{q}{\epsilon_{0}}
\]
Integral de \( \displaystyle \int_{0}^{{2\pi}}\;d\phi \)
\[
\int_{0}^{{2\pi}}\;d\phi=\left.\phi \;\right|_{\;0}^{\;2\pi }=2\pi-0=2\pi
\]
Integral de \( \displaystyle \int_{0}^{L}\;dz \)
\[
\int_{0}^{L}\;dz=\left.z\;\right|_{\;0}^{\;L}=L-0=L
\]
\[
\begin{gather}
E r .2\pi .L=\frac{q}{\epsilon_{0}}\\
E=\frac{q}{2\pi \epsilon _{0}rL} \tag{VII}
\end{gather}
\]
da expressão da densidade linear de cargas
\[ \bbox[#99CCFF,10px]
{\lambda=\frac{q}{L}}
\]
\[
\begin{gather}
q=\lambda L \tag{VIII}
\end{gather}
\]
substituindo a expressão (VIII) na expressão (VII)
\[
E=\frac{\lambda \cancel{L}}{2\pi \epsilon_{0}r\cancel{L}}
\]
\[ \bbox[#FFCCCC,10px]
{E=\frac{\lambda }{2\pi \epsilon_{0}r}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .