Exercício Resolvido de Força Elétrica e Campo Elétrico
publicidade
Considere dois anéis concêntricos e situados sobre o mesmo plano. O anel de raio R1 possui carga Q1, e o anel de raio R2 possui carga Q2. O vetor campo elétrico produzido por um anel de raio r a uma distância z do centro é dado por
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_0}\frac{Qz}{\left(r^2+z^2\right)^{3/2}}\;\mathbf{k}
\end{gather}
\]
Determine o vetor campo elétrico:a) No centro comum dos dois anéis;
b) Em um ponto situado a uma distância z muito maior do que R1, e do que R2.
Dados do problema:
- Raio do anel 1: R1;
- Carga do anel 1: Q1;
- Raio do anel 2: R2;
- Carga do anel 2: Q2.
Adotamos um sistema de referência com origem no centro dos anéis com R1>R2 (Figura 1-A).
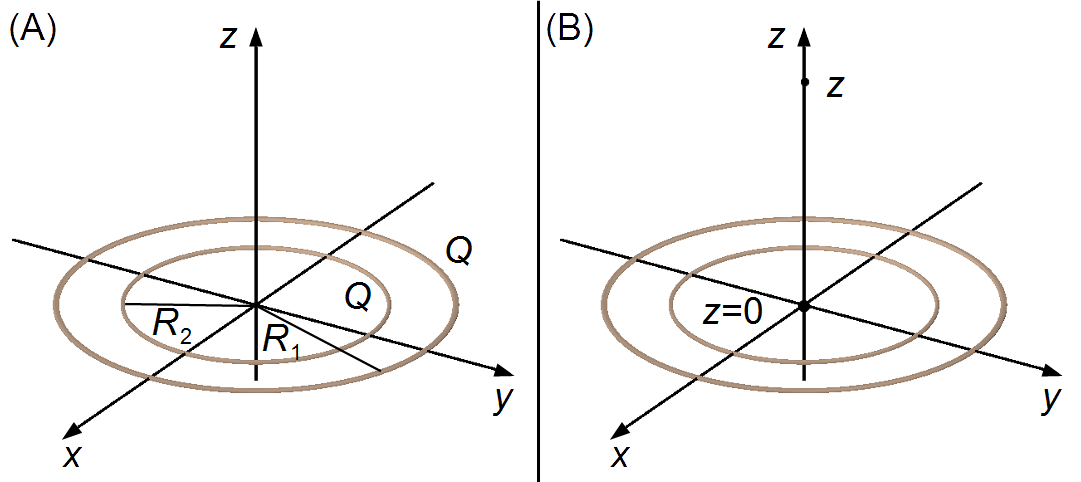
Queremos calcular o campo elétrico no centro comum aos dois anéis, na origem em z=0, e em um ponto z qualquer à uma distância muito maior do que os raios R1 e R2 dos anéis (Figura 1-B).
Solução
O vetor campo elétrico total é dado pela soma dos vetores campo elétrico produzido por cada um dos anéis
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{E}=\mathbf{E}_1+\mathbf{E}_2}
\end{gather}
\]
a) Para o anel 1 o vetor campo elétrico será
\[
\begin{gather}
\mathbf{E}_1=\frac{1}{4\pi \epsilon_0}\frac{Q_1\times0}{\left(R_1^2+0^2\right)^{3/2}}\;\mathbf{k}=0
\end{gather}
\]
Para o anel 2 o vetor campo elétrico será
\[
\begin{gather}
\mathbf{E}_2=\frac{1}{4\pi \epsilon_0}\frac{Q_1\times0}{\left(R_2^2+0^2\right)^{3/2}}\;\mathbf{k}=0
\end{gather}
\]
O vetor campo elétrico total será
\[
\begin{gather}
\mathbf{E}=0+0
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=0}
\end{gather}
\]
b) Para o anel 1 o vetor campo elétrico a uma distância z será
\[
\begin{gather}
\mathbf{E}_1=\frac{1}{4\pi \epsilon_0}\frac{Q_1z}{\left(R_1^2+z^2\right)^{3/2}}\;\mathbf{k}
\end{gather}
\]
se z≫R1 podemos desprezar o valor de R1
\[
\begin{gather}
\mathbf{E}_1=\frac{1}{4\pi \epsilon_0}\frac{Q_1z}{\left(z^2\right)^{3/2}}\;\mathbf{k}\\[5pt]
\mathbf{E}_1=\frac{1}{4\pi\epsilon_{0}}\frac{Q_1z}{z^{2\times{\frac{3}{2}}}}\;\mathbf{k}\\[5pt]
\mathbf{E}_1=\frac{1}{4\pi\epsilon_0}\frac{Q_1\cancel z}{z^{\cancelto{2}{3}}}\;\mathbf{k}\\[5pt]
\mathbf{E}_1=\frac{1}{4\pi\epsilon_0}\frac{Q_1}{z^2}\;\mathbf{k}
\end{gather}
\]
Para o anel 2 o vetor campo elétrico será
\[
\begin{gather}
\mathbf{E}_2=\frac{1}{4\pi \epsilon_0}\frac{Q_1z}{\left(R_2^2+z^2\right)^{3/2}}\;\mathbf{k}
\end{gather}
\]
se z≫R2 podemos desprezar o valor de R2
\[
\begin{gather}
\mathbf{E}_2=\frac{1}{4\pi \epsilon_0}\frac{Q_2z}{\left(z^2\right)^{3/2}}\;\mathbf{k}\\[5pt]
\mathbf{E}_2=\frac{1}{4\pi\epsilon_{0}}\frac{Q_2z}{z^{2\times{\frac{3}{2}}}}\;\mathbf{k}\\[5pt]
\mathbf{E}_2=\frac{1}{4\pi\epsilon_0}\frac{Q_2\cancel z}{z^{\cancelto{2}{3}}}\;\mathbf{k}\\[5pt]
\mathbf{E}_2=\frac{1}{4\pi\epsilon_0}\frac{Q_2}{z^2}\;\mathbf{k}
\end{gather}
\]
O vetor campo elétrico total será
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_0}\frac{Q_1}{z^2}\;\mathbf{k}+\frac{1}{4\pi\epsilon_{0}}\frac{Q_2}{z^2}\;\mathbf{k}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_0}\frac{\left(Q_1+Q_2\right)}{z^2}\;\mathbf{k}}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .