Exercício Resolvido de Força Elétrica e Campo Elétrico
publicidade
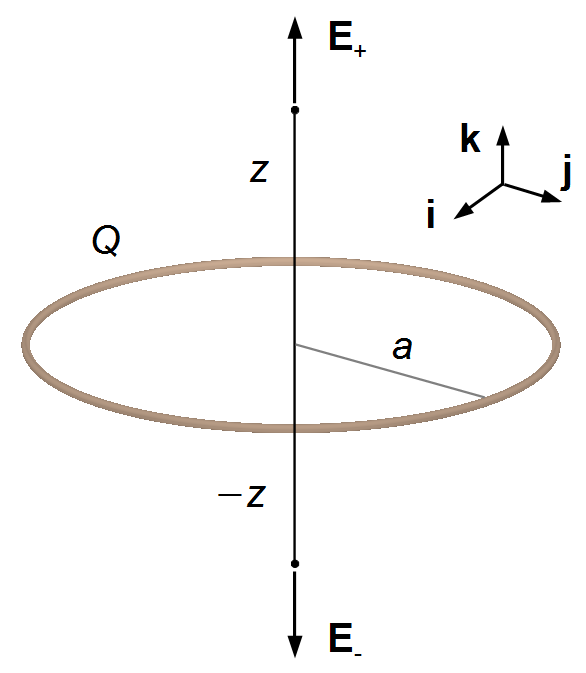
Uma aro de raio a está carregado uniformemente com uma carga Q. O campo elétrico produzido por este aro nos pontos sobre o eixo de simetria perpendicular ao plano do aro a uma distância z é dado, em módulo, por
\[
\begin{gather}
E=\frac{1}{4\pi \epsilon_{0}}\frac{Qz}{\left(a^{2}+z^{2}\right)^{3/2}}
\end{gather}
\]
Determine:
a) Para quais valores de z o campo elétrico é máximo;
b) Qual é este valor máximo.
Solução
a) Para encontramos o valor máximo do campo elétrico devemos derivar a função do campo elétrico em função de z, E(z), e igualar a zero
\[
\begin{gather}
\frac{dE}{dz}=0
\end{gather}
\]
Derivada de \( \displaystyle E(z)=\frac{1}{4\pi \epsilon_{0}}\frac{Qz}{\left(a^{2}+z^{2}\right)^{3/2}} \)
A função E(z) é o quociente de dua funções, usando a regra da derivada do quociente
A função E(z) é o quociente de dua funções, usando a regra da derivada do quociente
\[
\begin{gather}
\left(\frac{u}{v}\right)^{'}=\frac{u'v-uv'}{v^{2}}
\end{gather}
\]
onde
\( u(z)=z \)
e
\( v(z)=\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}} \)
\[
\begin{gather}
\frac{dE}{dz}=\frac{Q}{4\pi \epsilon_{0}}\frac{\dfrac{d(z)}{dz}\left(a^{2}+z^{2}\right)^{3/2}-(z)\dfrac{d\left[\left(a^{2}+z^{2}\right)^{3/2}\right]}{dz}}{\left[\left(a^{2}+z^{2}\right)^{3/2}\right]^{2}}
\end{gather}
\]
a função v(z) é uma função composta, usando a Regra da Cadeia
\[
\begin{gather}
\frac{dv[w(z)]}{dz}=\frac{dv}{dw}\frac{dw}{dz}
\end{gather}
\]
onde
\( v(w)=w^{3/2} \)
e
\( w(z)=a^{2}+z^{2} \)
\[
\begin{gather}
\frac{dE}{dz}=\frac{Q}{4\pi \epsilon_{0}}\frac{1.\left(a^{2}+z^{2}\right)^{3/2}-z\left[\dfrac{d\left(w^{3/2}\right)}{dg}\dfrac{d\left(a^{2}+z^{2}\right)}{dz}\right]}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\frac{\left(a^{2}+z^{2}\right)^{3/2}-z\left[\left(\dfrac{3}{2}w^{\frac{3}{2}-1}\right)(2z)\right]}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\frac{\left(a^{2}+z^{2}\right)^{3/2}-z\dfrac{3}{\cancel{2}}\left(a^{2}+z^{2}\right)^{1/2}\cancel{2}z}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\frac{\left(a^{2}+z^{2}\right)^{3/2}-3\left(a^{2}+z^{2}\right)^{1/2}z^{2}}{\left(a^{2}+z^{2}\right)^{3}}\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\left[\frac{\left(a^{2}+z^{2}\right)^{3/2}}{\left(a^{2}+z^{2}\right)^{3}}-\frac{3\left(a^{2}+z^{2}\right)^{1/2}z^{2}}{\left(a^{2}+z^{2}\right)^{3}}\right]\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\left[\frac{1}{\left(a^{2}+z^{2}\right)^{3}\left(a^{2}+z^{2}\right)^{-3/2}}-\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{3}\left(a^{2}+z^{2}\right)^{-1/2}}\right]\\[5pt]
\frac{dE}{dz}=\frac{Q}{4\pi\epsilon_{0}}\left[\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}}-\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{5/2}}\right]
\end{gather}
\]
Igualando a derivada a zero
\[
\begin{gather}
\frac{Q}{4\pi \epsilon_{0}}\left[\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}}-\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{5/2}}\right]=0\\[5pt]
\frac{1}{\left(a^{2}+z^{2}\right)^{3/2}}=\frac{3z^{2}}{\left(a^{2}+z^{2}\right)^{5/2}}\\[5pt]
\frac{\left(a^{2}+z^{2}\right)^{5/2}}{\left(a^{2}+z^{2}\right)^{3/2}}=3z^{2}\\[5pt]
\left(a^{2}+z^{2}\right)^{5/2}\left(a^{2}+z^{2}\right)^{-3/2}=3z^{2}\\[5pt]
\left(a^{2}+z^{2}\right)^{\frac{5}{2}-\frac{3}{2}}=3z^{2}\\[5pt]\left(a^{2}+z^{2}\right)^{\frac{2}{2}}=3z^{2}\\[5pt]
a^{2}+z^{2}=3z^{2}\\[5pt]
3z^{2}-z^{2}=a^{2}\\[5pt]
z^{2}=\frac{a^{2}}{2}\\[5pt]
z=\sqrt{\frac{a^{2}}{2}}\\[5pt]
z=\pm{\frac{a}{\sqrt{2}}.\frac{\sqrt{2}}{\sqrt{2}}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{z=\frac{a\sqrt{2}}{2}}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{z=-{\frac{a\sqrt{2}}{2}}}
\end{gather}
\]
b) Substituindo os valores de z encontrados no item (a) na expressão dada no problema
\[
\begin{gather}
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi \epsilon_{0}}\frac{Q\dfrac{a\sqrt{2}}{2}}{\left[a^{2}+\left(\dfrac{a\sqrt{2}}{2}\right)^{2}\right]^{3/2}}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\left[a^{2}+\dfrac{a^{2}}{2}\right]^{3/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\left[\dfrac{2a^{2}+a^{2}}{2}\right]^{3/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\left[\dfrac{3a^{2}}{2}\right]^{3/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\dfrac{3a^{2}}{2}\left[\dfrac{3a^{2}}{2}\right]^{1/2}}\frac{a\sqrt{2}}{2}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{\dfrac{3a^{2}}{\cancel{2}}\dfrac{\cancel{a}\sqrt{3}}{\sqrt{2}}}\frac{\cancel{a}\sqrt{2}}{\cancel{2}}\\[5pt]
E\left(\frac{a\sqrt{2}}{2}\right)=\frac{1}{4\pi\epsilon_{0}}\frac{Q}{3a^{2}\sqrt{3}}\sqrt{2}.\sqrt{2}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{E=\frac{1}{4\pi \epsilon _{0}}\frac{2Q}{3\sqrt{3}a^{2}}}
\end{gather}
\]
Observação: O cálculo feito com o valor
\( z=-{\frac{a\sqrt{2}}{2}} \)
dá o resultado
\[
\begin{gather}
E=-{\frac{1}{4\pi \epsilon_{0}}}\frac{2Q}{3\sqrt{3}a^{2}}
\end{gather}
\]
o sinal de negativo indica que o vetor campo elétrico está apontanto na direção oposta ao vetor
unitário k (Fighra 1).
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .