Exercício Resolvido de Campo Elétrico
Português
English
publicidade
Determine o torque que atua sobre um dipolo elétrico imerso num campo elétrico uniforme. Determine também a
energia potência deste dipolo.
Esquema do problema:
O dipolo é formado por cargas de mesmo valor e sinais contrários, +q e −q, colocadas em um campo elétrico uniforme E. Na carga positiva atua uma força elétrica FE no mesmo sentido do campo elétrico e na carga negativa atua uma força elétrica mesma intensidade e sentido oposto ao campo elétrico (Figura 1-A).
Adotamos um sistema de referência xyz com origem no centro do dipolo, onde i, j e k são os vetores unitários nas direções x, y e z (Figura 1-A)
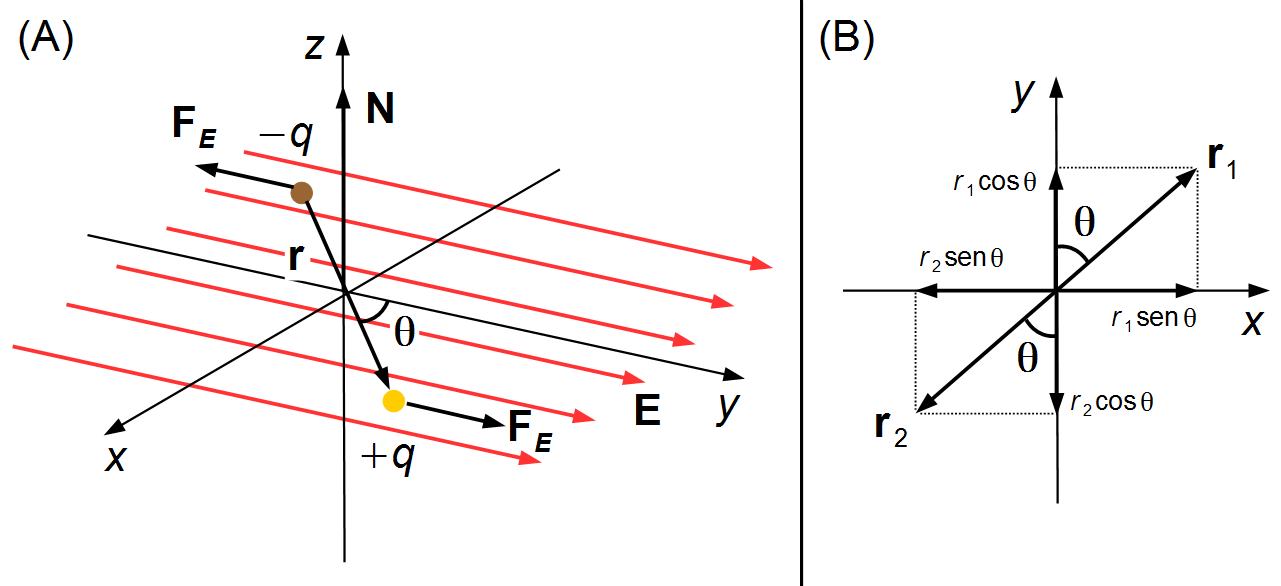Figura 1
O vetor r1 localiza a carga elétrica +q e \( r_{1}=\frac{d}{2} \), o vetor r2 localiza a carga elétrica −q e \( r_{2}=\frac{d}{2} \). O momento de dipolo é definido como apontando da carga negativa para a carga positiva dado pelo vetor posição r (Figuras 1-A e 1-B)
Sob a ação do par de forças elétricas este sistema gira sob a ação de um torque dado por
Substituindo \( \mathbf{N}=0\;\mathbf{i}+0\;\mathbf{j}+pE\operatorname{sen}\theta\;\mathbf{k} \) e \( d\mathbf{\theta}=0\;\mathbf{i}+0\;\mathbf{j}+d\theta\;\mathbf{k} \) na expressão (VI) e calculando o produto escalar
O trabalho é armazenado na forma de energia potencial do sistema
podemos escrever
Esquema do problema:
O dipolo é formado por cargas de mesmo valor e sinais contrários, +q e −q, colocadas em um campo elétrico uniforme E. Na carga positiva atua uma força elétrica FE no mesmo sentido do campo elétrico e na carga negativa atua uma força elétrica mesma intensidade e sentido oposto ao campo elétrico (Figura 1-A).
Adotamos um sistema de referência xyz com origem no centro do dipolo, onde i, j e k são os vetores unitários nas direções x, y e z (Figura 1-A)
O vetor r1 localiza a carga elétrica +q e \( r_{1}=\frac{d}{2} \), o vetor r2 localiza a carga elétrica −q e \( r_{2}=\frac{d}{2} \). O momento de dipolo é definido como apontando da carga negativa para a carga positiva dado pelo vetor posição r (Figuras 1-A e 1-B)
\[
\begin{gather}
{\mathbf{r}}_{1}=r_{1}\operatorname{sen}\theta\;\mathbf{i}+r_{1}\cos \theta\;\mathbf{j}\\[5pt]
{\mathbf{r}}_{1}=\frac{d}{2}\operatorname{sen}\theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}
\end{gather}
\]
\[
\begin{gather}
{\mathbf{r}}_{2}=-r_{2}\operatorname{sen}\theta\;\mathbf{i}-r_{2}\cos \theta\;\mathbf{j}\\[5pt]
{\mathbf{r}}_{2}=-{\frac{d}{2}}\operatorname{sen}\theta\;\mathbf{i}-\frac{d}{2}\cos \theta\;\mathbf{j}
\end{gather}
\]
\[
\begin{gather}
\mathbf{r}={\mathbf{r}}_{1}-{\mathbf{r}}_{2}\\[5pt]
\mathbf{r}=\frac{d}{2}\operatorname{sen}\theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}-\left(-{\frac{d}{2}}\operatorname{sen}\theta\;\mathbf{i}-\frac{d}{2}\cos \theta\;\mathbf{j}\right)\\[5pt]
\mathbf{r}=\frac{d}{2}\operatorname{sen}\theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}+\frac{d}{2}\operatorname{sen}\theta\;\mathbf{i}+\frac{d}{2}\cos \theta\;\mathbf{j}\\[5pt]
\mathbf{r}=d\operatorname{sen}\theta\;\mathbf{i}+d\cos \theta\;\mathbf{j}
\end{gather}
\]
Solução
Sob a ação do par de forças elétricas este sistema gira sob a ação de um torque dado por
\[ \bbox[#99CCFF,10px]
{\mathbf{N}=\mathbf{r}\times{\mathbf{F}}}
\]
a única força que atua no sistema é a força elétrica FE
\[
\begin{gather}
\mathbf{N}=\mathbf{r}\times{\mathbf{F}}_{E} \tag{I}
\end{gather}
\]
A força elétrica é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{{\mathbf{F}}_{E}=q\mathbf{E}} \tag{II}
\end{gather}
\]
substituindo a expressão (II) na expressão (I)
\[
\begin{gather}
\mathbf{N}=\mathbf{r}\times q\mathbf{E}\\
\mathbf{N}=q\mathbf{r}\times{\mathbf{E}} \tag{III}
\end{gather}
\]
O momento de dipolo é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{p}=q\mathbf{r}} \tag{IV}
\end{gather}
\]
substituindo a expressão (IV) na expressão (III)
\[ \bbox[#FFCCCC,10px]
{\mathbf{N}=\mathbf{p}\times{\mathbf{E}}}
\]
O campo elétrico está apontado na direção j
\[
\mathbf{E}=E\;\mathbf{j}
\]
e o momento de dipolo pode ser escrito como
\[
\mathbf{p}=q(d\operatorname{sen}\theta\;\mathbf{i}+d\cos \theta \;\mathbf{j})
\]
o torque pode ser escrito como
\[
\begin{gather}
\mathbf{p}\times{\mathbf{E}}=\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}\\
qd\operatorname{sen}\theta & qd\cos \theta & 0\\
0 & E &0
\end{matrix}\right|=\\[5pt]
=\left[qd\cos\theta.0-0.E\right]\;\mathbf{i}-\left[qd\operatorname{sen}\theta.0-0.0\right]\;\mathbf{j}+\left[qdE\operatorname{sen}\theta-0. qdE\right]\;\mathbf{k}\\[5pt]
\mathbf{p}\times{\mathbf{E}}=qEd\operatorname{sen}\theta\;\mathbf{k} \tag{V}
\end{gather}
\]
\[
\mathbf{N}=qEd\operatorname{sen}\theta\;\mathbf{k}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{N}=pE\operatorname{sen}\theta\;\mathbf{k}}
\]
O trabalho de uma força é dado por
\[ \bbox[#99CCFF,10px]
{W=\int {\mathbf{F}}\cdot d\mathbf{r}}
\]
para um corpo girando a força é dada pelo torque F = N e o deslocamento é dado pelo
deslocamento angular dr = dθ
\[
\begin{gather}
W=\int {\mathbf{N}}\cdot d\mathbf{\theta } \tag{VI}
\end{gather}
\]
o vetor deslocamento angular é dado por
\[
d\mathbf{\theta }=d\theta \;\mathbf{k}
\]
Observação: Algumas pessoas acham dífícil entender que o vetor deslocamento angular aponte
na direção k perpendicularmente ao plano de rotação. Quando um corpo se desloca de uma posição
r para uma posição r' temos um deslocamento infinitesimal ds ao longo da
trajetória, o deslocamento angular dθ está contido no plano, mas o vetor deslocamento
angular dθ aponta perpendicularmente ao plano, isto preserva o produtor vetorial
(Figura 2). O vetor deslocamento angular indica que o corpo está em rotação, o seu módulo indica o
deslocamento angular (escalar) e o sentido do vetor indica o sentido de rotação do corpo, se o vetor
dθ é positivo o produto vetorial indica que o corpo está se deslocando no sentido
horário, se for negativo o corpo está se deslocando no sentido anti-horário.
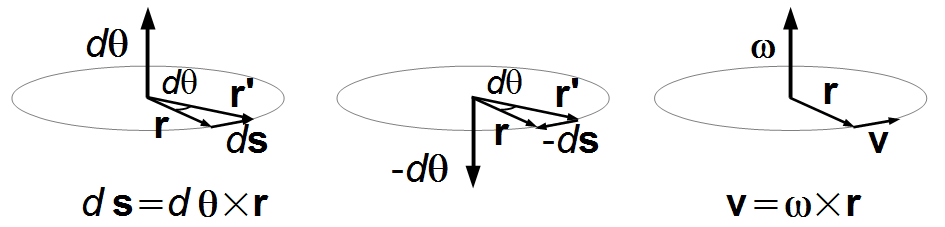Figura 2
Este é o mesmo argumento usado para a velocidade angular, o vetor velocidade v é tangente à trajetória, mas o vetor velocidade angular ω é perpendicular à trajetória.
Este é o mesmo argumento usado para a velocidade angular, o vetor velocidade v é tangente à trajetória, mas o vetor velocidade angular ω é perpendicular à trajetória.
Substituindo \( \mathbf{N}=0\;\mathbf{i}+0\;\mathbf{j}+pE\operatorname{sen}\theta\;\mathbf{k} \) e \( d\mathbf{\theta}=0\;\mathbf{i}+0\;\mathbf{j}+d\theta\;\mathbf{k} \) na expressão (VI) e calculando o produto escalar
\[
\begin{gather}
W=\int(0\;\mathbf{i}+0\;\mathbf{j}+pE\operatorname{sen}\theta\;\mathbf{k})\dot{\;}(0\;\mathbf{i}+0\;\mathbf{j}+d\theta\;\mathbf{k})\\[5pt]
W=\int0.0\;\underbrace{\mathbf{i}.\mathbf{i}}_{1}+0.0\;\underbrace{\mathbf{j}.\mathbf{j}}_{1}+pE\operatorname{sen}\theta d\theta\;\underbrace{\mathbf{k}.\mathbf{k}}_{1}\\[5pt]
W=\int pE\operatorname{sen}\theta \;d\theta \\W=pE\int_{\theta_{0}}^{\theta}\operatorname{sen}\theta \;d\theta \\[5pt]
W=pE\left.\left(-\cos \theta\right)\right|_{\;\theta _{0}}^{\;\theta }\\[5pt]
W=-pE\left(\cos \theta-\cos \theta _{0}\right)
\end{gather}
\]
Observação: Como i é um vetor unitário seu módulos é igual a 1 e o ângulo com o
próprio vetor é nulo (θ = 0 ), assim
\( \mathbf{i}.\mathbf{i}=|\;\mathbf{i}\;|\;|\;\mathbf{i}\;|\cos0=1.1.1=1 \).
O trabalho é armazenado na forma de energia potencial do sistema
\[
\begin{gather}
W=\Delta U\\
\Delta U=-pE(\cos \theta -\cos \theta_{0})
\end{gather}
\]
escolhendo para situação inicial
\( \theta_{0}=\frac{\pi}{2}\Rightarrow \cos \theta_{0}=0 \)
\[ \bbox[#FFCCCC,10px]
{U=-pE\cos \theta}
\]
Usando a definição do Produto Escalar
\[
c=|\;a\;||\;b\;|\cos \theta
\]
\[
c=\mathbf{a}\cdot {\mathbf{b}}
\]
podemos escrever
\[ \bbox[#FFCCCC,10px]
{U=-{\mathbf{p}}\cdot {\mathbf{E}}}
\]
publicidade
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .