Exercício Resolvido de Força Elétrica e Campo Elétrico
Português
English
publicidade
Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito.
Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio.
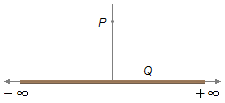
Dados do problema:
- Carga do fio: Q.
O vetor posição r vai de um elemento de carga dq do fio até o ponto P onde se deseja calcular o campo elétrico, o vetor rq localiza o elemento de carga em relação à origem do referencial e o vetor rp localiza o ponto P (Figura1-A).
\[
\mathbf{r}={\mathbf{r}}_{p}-{\mathbf{r}}_{q}
\]
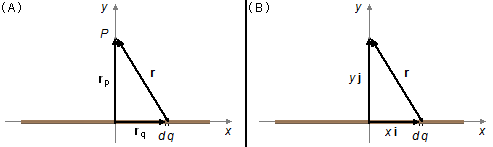
Pela geometria do problema devemos escolher coordenadas cartesianas, o vetor rq só possui componente na direção i, é escrito como \( {\mathbf{r}}_{q}=x\;\mathbf{i} \) e o vetor rp só possui componente na direção j, é escrito como \( {\mathbf{r}}_{p}=y\;\mathbf{j} \) (Figura 1-B), então o vetor posição será
\[
\begin{gather}
\mathbf{r}=y\;\mathbf{j}-x\;\mathbf{i} \tag{I}
\end{gather}
\]
Da expressão (I) o módulo do vetor posição r será
\[
\begin{gather}
r^{2}=(-x)^{2}+y^{2}\\
r=\left(x^{2}+y^{2}\right)^{\frac{1}{2}} \tag{II}
\end{gather}
\]
Solução
O vetor campo elétrico do fio é dado por
\[ \bbox[#99CCFF,10px]
{\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{2}}\;\frac{\mathbf{r}}{r}}}
\]
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int{\frac{dq}{r^{3}}\;\mathbf{r}} \tag{III}
\end{gather}
\]
Da expressão da densidade linear de carga λ obtemos o elemento de carga dq
\[ \bbox[#99CCFF,10px]
{\lambda =\frac{dq}{ds}}
\]
\[
\begin{gather}
dq=\lambda \;ds \tag{IV}
\end{gather}
\]
onde ds é um elemento de comprimento do fio
\[
\begin{gather}
ds=dx \tag{V}
\end{gather}
\]
substituindo a expressão (V) na expressão (IV)
\[
\begin{gather}
dq=\lambda \;dx \tag{VI}
\end{gather}
\]
Substituindo as expressões (I), (II) e (VI) na expressão (III)
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_{0}}\int {\frac{\lambda\;dx}{\left[\left(x^{2}+y^{2}\right)^{\frac{1}{2}}\right]^{3}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)\\
\mathbf{E}=\frac{1}{4\pi\epsilon_{0}}\int {\frac{\lambda\;dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right) \tag{VII}
\end{gather}
\]
Como a densidade de carga λ é constante ela pode “sair” da integral
\[
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int{\frac{dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)
\]
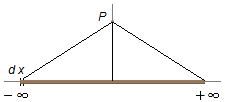
O vetor posição r que vai de um elemento de carga dq até o ponto
P deve varrer todo o fio de −∞ a +∞ (Figura 2).
\[
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{{\infty}}{\frac{dx}{\left(x^{2}+y^{2}\right)^{\frac{3}{2}}}}\left(-x\;\mathbf{i}+y\;\mathbf{j}\right)
\]
colocando y em evidência no numerador e y2 no denominador
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{{\infty}}{\frac{dx}{\left[y^{2}\left(1+\dfrac{x^{2}}{y^{2}}\right)\right]^{\frac{3}{2}}}}y\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{{\infty}}{\frac{dx}{\left(y^{2}\right)^{\frac{3}{2}}\left[1+\left(\dfrac{x}{y}\right)^{2}\right]^{\frac{3}{2}}}}y\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{{\infty}}{\frac{dx}{y^{\cancelto{2}{3}}\left[1+\left(\dfrac{x}{y}\right)^{2}\;\right]^{\frac{3}{2}}}}\cancel{y}\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{{\infty}}{\frac{dx}{y^{2}\left[1+\left(\dfrac{x}{y}\right)^{2}\right]^{\frac{3}{2}}}}\left(-{\frac{x}{y}}\;\mathbf{i}+\;\mathbf{j}\right) \tag{VIII}
\end{gather}
\]
Considerando o ângulo θ medido entre o eixo-y e a distância r do elemento de carga
dq ao ponto P, a tangente deste ângulo será (Figura 3)
\[
\begin{gather}
\operatorname{tg}\theta =\frac{x}{y} \\
x=y\operatorname{tg}\theta \tag{IX}
\end{gather}
\]
substituindo a expressão (IX) na expressão (VIII)
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\dfrac{\cancel{y}\operatorname{tg}\theta}{\cancel{y}}\right)^{2}\right]^{\frac{3}{2}}}}\left(-{\frac{\cancel{y}\operatorname{tg}\theta}{\cancel{y}}}\;\mathbf{i}+\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{dx}{y^{2}\left[1+\left(\operatorname{tg}\theta\right)^{2}\right]^{\frac{3}{2}}}}\left(-\operatorname{tg}\theta\;\mathbf{i}+\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-{\frac{L}{2}}}}^{{\frac{L}{2}}}{\frac{\mathit{dx}}{y^{2}\left(1+\operatorname{tg}^{2}\theta\right)^{\frac{3}{2}}}}\left(-\operatorname{tg}\theta\;\mathbf{i}+\;\mathbf{j}\right) \tag{X}
\end{gather}
\]
A partir da expressão (IX) obtemos o elemento de comprimento dx em relação ao elemento de arco
dθ.
Derivada de
\( x=y\operatorname{tg}\theta \)
\[
\frac{dx}{d\theta}=y\frac{d}{d\theta}\left(\operatorname{tg}\theta \right)
\]
reescrevendo
\( \operatorname{tg}\theta=\dfrac{\operatorname{sen}\theta}{\cos \theta} \),
temos a derivada de um quociente de funções dada pela fórmula
\[
\left(\frac{u}{v}\right)^{\Large '}=\frac{u'v-u\;v'}{v^{2}}
\]
\[
\begin{align}
\frac{d}{d\theta}\left(\operatorname{tg}\theta \right)=\frac{d}{d\theta}\left(\frac{\operatorname{sen}\theta}{\cos \theta}\right) &=\frac{\cos\theta \cos \theta-\operatorname{sen}\theta (-\operatorname{sen}\theta)}{(\cos \theta)^{2}}=\\
&=\frac{\cos ^{2}\theta+\operatorname{sen}^{2}\theta}{\cos ^{2}\theta}=\frac{1}{\cos^{2}\theta}
\end{align}
\]
\[
\begin{gather}
\frac{dx}{d\theta}=y\frac{1}{\cos ^{2}\theta}
\end{gather}
\]
Observação: Via de regra os livros de
Cálculo Integral e Diferencial apresentam a derivada da tangente na forma
\( \left(\operatorname{tg}\theta \right)^{'}=\operatorname{sec}^{2}\theta \),
onde
\( \operatorname{sec}\theta=\dfrac{1}{\cos \theta} \),
mas aqui por razões de simplificações posteriores vamos deixar a derivada na
forma mostrada acima.
\[
\begin{gather}
dx=y\frac{1}{\cos ^{2}\theta}\;d\theta \tag{XI}
\end{gather}
\]
substituindo a definição da tangente e a expressão (XI) na expressão (X)
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{\infty}{\frac{1}{y^{\cancel{2}}\left[1+\left(\dfrac{\operatorname{sen}\theta}{\cos \theta}\;\right)^{2}\;\right]^{\frac{3}{2}}}}\cancel{y}\;\frac{d\theta}{\cos^{2}\theta}\;\left(\;-\frac{\operatorname{sen}\theta}{\cos \theta}\;\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{{-\infty}}^{\infty}{\frac{1}{y\left[1+\left(\dfrac{\operatorname{sen}\theta}{\cos \theta}\;\right)^{2}\;\right]^{\frac{3}{2}}}}\;\frac{d\theta}{\cos^{2}\theta}\;\left(\;-\frac{\operatorname{sen}\theta}{\cos \theta}\;\mathbf{i}+\;\mathbf{j}\;\right)
\end{gather}
\]
O vetor posição r que vai de um elemento de carga dq até o ponto P forma um ângulo
θ com o eixo-y. Conforme o elemento dq se desloca da origem em direção a ±∞
o ângulo vai aumento e tende a
\( \frac{\pi}{2} \).
Os extremos de integração para a variável θ devem variar de
\( -{\frac{\pi}{2}} \),
o valor máximo medido no sentido horário, quando x vale −∞ até
\( \frac{\pi}{2} \)
o valor máximo medido no sentido anti-horário, quando x vale +∞ (Figura 4).
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{1}{y\left(1+\dfrac{\operatorname{sen}^{2}\theta}{\cos^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\operatorname{sen}\theta}{\cos\theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{1}{y\left(\dfrac{\cos ^{2}+\operatorname{sen}^{2}\theta}{\cos ^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos^{2}\theta}\;\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{1}{y\left(\dfrac{1}{\cos ^{2}\theta}\right)^{\frac{3}{2}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{1}{y\dfrac{1}{\left(\cos ^{2}\theta\right)^{\frac{3}{2}}}}}\;\frac{d\theta}{\cos ^{2}\theta}\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}\;}\mathbf{i}+\;\mathbf{j}\;\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{1}{y\dfrac{1}{\cos ^{\cancel{3}}\theta}}}\;\frac{d\theta}{\cancel{\cos^{2}\theta}}\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{1}{y\dfrac{1}{\cos \theta}}}\;d\theta\left(-{\frac{\operatorname{sen}\theta}{\cos \theta}}\;\mathbf{i}+\;\mathbf{j}\right)\\[5pt]
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}}\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}{\frac{\cos\theta}{y}}\;d\theta \left(-{\frac{\operatorname{sen}\theta}{\cos\theta}}\;\mathbf{i}+\;\mathbf{j}\right)
\end{gather}
\]
Como y é constante, a integral depende só de θ, ele pode “sair” da integral e a integral da
soma é igual à soma das integrais
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0} y}\left(-\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}\cos \theta\frac{\operatorname{sen}\theta}{\cos \theta}\;d\theta\;\mathbf{i}+\int_{-{\frac{\pi}{2}}}^{{\frac{\pi}{2}}}\cos\theta \;d\theta\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}\left(\underbrace{-{\int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}\operatorname{sen}\theta \;d\theta\;\mathbf{i}}}_{0}+\int_{-{\frac{\pi}{2}}}^{{\frac{\pi}{2}}}\cos \theta \;d\theta\;\mathbf{j}\right)
\end{gather}
\]
Integral de \( \displaystyle \int_{-{\frac{\pi}{2}}}^{\frac{\pi}{2}}\cos \theta \;d\theta \)
1.º método
Como a função cosseno é uma função par, f(x) = f(−x), podemos integrar sobre metade do intervalo \( \left(\;\text{de }0\text{ a }\frac{\pi}{2}\;\right) \) e multiplicar a integral por 2
Podemos integrar sobre todo intervalo \( \left(\;\text{de }-\frac{\pi}{2}\text{ a }\frac{\pi}{2}\;\right) \)
1.º método
Como a função cosseno é uma função par, f(x) = f(−x), podemos integrar sobre metade do intervalo \( \left(\;\text{de }0\text{ a }\frac{\pi}{2}\;\right) \) e multiplicar a integral por 2
\[
\begin{align}
2\int_{0}^{{\frac{\pi}{2}}}\cos \theta \;d\theta &=2\left.\operatorname{sen}\theta \;\right|_{\;0}^{\;\frac{\pi}{2}}=2\left(\operatorname{sen}\frac{\pi}{2}-\operatorname{sen}0\right)=\\
&=2(1-0)=2
\end{align}
\]
2.º método
Podemos integrar sobre todo intervalo \( \left(\;\text{de }-\frac{\pi}{2}\text{ a }\frac{\pi}{2}\;\right) \)
\[
\int_{{-{\frac{\pi}{2}}}}^{{\frac{\pi}{2}}}\cos \theta \;d\theta=\left.\operatorname{sen}\theta \;\right|_{\;-\frac{\pi}{2}}^{\;\frac{\pi}{2}}=\operatorname{sen}\frac{\pi}{2}-\operatorname{sen}\left(-{\frac{\pi}{2}}\right)
\]
como seno é uma função ímpar, f(−x) = −f(x), temos que
\( \operatorname{sen}\left(-{\frac{\pi}{2}}\right)=-\operatorname{sen}\frac{\pi}{2} \)
\[
\begin{align}
\int_{{-{\frac{\pi}{2}}}}^{{\frac{\pi}{2}}}\cos \theta \;d\theta &=\operatorname{sen}\frac{\pi}{2}-\left(-\operatorname{sen}\frac{\pi}{2}\right)=\\
&=\operatorname{sen}\frac{\pi}{2}+\operatorname{sen}\frac{\pi}{2}=1+1=2
\end{align}
\]
Integral de \( \displaystyle \int_{{-{\frac{\pi}{2}}}}^{{\frac{\pi}{2}}}\operatorname{sen}\theta\;d\theta \)
1.º método
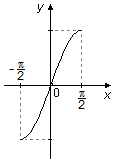
Figura 5
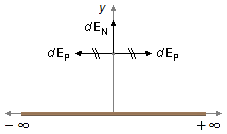Figura 6
1.º método
\[
\int_{{-{\frac{\pi}{2}}}}^{{\frac{\pi}{2}}}\operatorname{sen}\theta \;d\theta =-\left.\cos \theta\;\right|_{\;-\frac{\pi}{2}}^{\;\frac{\pi}{2}}=-\left[\cos \frac{\pi}{2}-\cos \left(-{\frac{\pi}{2}}\right)\right]
\]
como cosseno é uma função par, f(x) = f(−x)
\( \cos \frac{\pi}{2}=\cos \left(-{\frac{\pi}{2}}\right) \)
\[
\int_{{-{\frac{\pi}{2}}}}^{{\frac{\pi}{2}}}\operatorname{sen}\theta\;d\theta =-\left(\cos \frac{\pi}{2}-\cos \frac{\pi}{2}\right)=0
\]
2.º método
O gráfico do seno entre \( -{\frac{\pi}{2}} \) e 0 possui uma área “negativa” abaixo do eixo-x, e entre 0 e \( \frac{\pi}{2} \) uma área “positiva” acima do eixo-x, estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero. na direção i (Figura 5).
O gráfico do seno entre \( -{\frac{\pi}{2}} \) e 0 possui uma área “negativa” abaixo do eixo-x, e entre 0 e \( \frac{\pi}{2} \) uma área “positiva” acima do eixo-x, estas duas áreas se cancelam no cálculo da integral, sendo o valor da integral zero. na direção i (Figura 5).
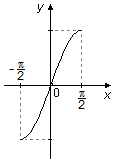
Figura 5
Observação: A integral na direção i, que é nula, representa o
cálculo matemático para a afirmação que se faz usualmente de que as componentes do
campo elétrico paralelas ao eixo-x,
dEP, se anulam. Apenas as componentes normais ao
eixo-x dEN contribuem para o campo elétrico
total (Figura 6).
\[
\begin{gather}
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}\left(-0\;\mathbf{i}+2\;\mathbf{j}\right)\\
\mathbf{E}=\frac{\lambda}{4\pi \epsilon_{0}y}2\;\mathbf{j}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\mathbf{E}=\frac{\lambda}{2\pi \epsilon_{0}y}\;\mathbf{j}}
\]
publicidade
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .