Exercício Resolvido de Movimento Unidimensional
publicidade

De duas cidadezinhas, ligadas por uma estrada reta de 10 km de comprimento, partem duas carroças, puxada cada uma por um cavalo e andando a velocidade de 5 km/h. No instante da partida, uma mosca, que estava pousada na testa do primeiro cavalo, parte voando em linha reta, com velocidade de 15 km/h e vai pousar na testa do segundo cavalo. Após um instante desprezível, parte novamente e volta, com a mesma velocidade de antes, em direção ao primeiro cavalo, até pousar em sua testa. E assim prossegue nesse vaivém até que os dois cavalos se encontram e a mosca morre esmagada entre as duas testas. Quantos quilômetros percorreu a mosca?

Dados do problema:

  • Distância entre as duas cidades: ΔS = 10 km;
  • Velocidade do primeiro cavalo: v1 = 5 km/h;
  • Velocidade do segundo cavalo: v2 = 5 km/h;
  • Velocidade da mosca: vm = 15 km/h.

Esquema do problema:

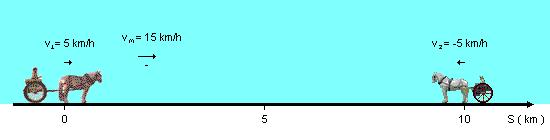
Adotamos um sistema de referência orientado para a direita com origem na posição do cavalo 1 (Figura 1), o cavalo 2 está se movendo contra a orientação da trajetória,

Figura 1

Solução:

Desejamos encontrar a distância total percorrida pela mosca Sm.

Observação: No problema usamos vm para indicar a velocidade da mosca, não confundir com velocidade média.

O primeiro cavalo está partindo da origem, posição inicial S01 = 0, o sinal positivo da velocidade indica que ele se move no mesmo sentido da orientação da trajetória. O segundo cavalo está partindo da outra cidade 10 km distante, S02 = 10 km, ele se move no sentido oposto da orientação da trajetória, sua velocidade é negativa, v2 = −5 km/h. A mosca também parte da origem, S0m = 0, e ela também se moveo no sentido de orientação da trajetória e sua velocidade é positiva.
A mosca vai voar entre os dois cavalos até estes se encontrarem. A primeira coisa que temos que determinar é o intervalo de tempo que os cavalos levam até o encontro dos dois. Escrevemos a equação do movimento de cada cavalo, como suas velocidades são constantes eles estão em Movimento Retilíneo Uniforme (M.R.U.), dada pela equação

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+vt } \tag{I} \end{gather} \]

aplicando a equação (I) para cada um dos cavalos

\[ \begin{gather} S_{1}=S_{01}+v_{1}t\\ S_{1}=0+5t\\ S_{1}=5t \tag{II-a} \end{gather} \]
\[ \begin{gather} S_{2}=S_{02}+v_{2}t\\ S_{2}=10-5t \tag{II-b} \end{gather} \]

Os dois cavalos se encontram quando ocupam a mesma posição, impondo a condição de igualdade entre as equações (II-a) e (II-b)

\[ \begin{gather} S_{1}=S_{2}\\ 5t=10-5t\\ 5t+5t=10\\ 10t=10\\ t=\frac{10}{10}\\ t=1\;\mathrm h \tag{III} \end{gather} \]

Aplicando a equação (I) para a mosca

\[ \begin{gather} S_{m}=S_{0m}+v_{m}t\\ S_{m}=0+15t\\ S_{m}=15t \tag{IV} \end{gather} \]

para sabermos quantos quilômetros a mosca percorreu substituímos o intervalo de tempo que os cavalos levam para se encontrar, encontrado na equação (IV), na equação (V)

\[ \begin{gather} S_{m}=15.1\\ S_{m}=15\;\mathrm{km} \end{gather} \]

A mosca percorrerá 15 km até ser esmagada pelos cavalos.

publicidade