Exercício Resolvido de Movimento Unidimensional
publicidade   



Um corpo é abandonado no vácuo de uma altura H. Calcular H sabendo que o corpo percorre os últimos h metros em T segundos. A aceleração da gravidade é g.


Dados do problema:
  • Altura da queda:    H;
  • Espaço inicial da parte final da trajetória:    S0 = h;
  • Espaço final:    S = 0;
  • Intervalo de tempo para percorrer o final da trajetória:    T;
  • Aceleração da gravidade:    g.
Esquema do problema:

Adotando-se um sistema de referência orientado para cima, o espaço inicial será a altura H de onde objeto é solto, o espaço final será a origem (zero), h é a altura em que o corpo está ao se contar o tempo final da queda, a aceleração da gravidade e a velocidade terão sinal negativo, estão no sentido contrário à orientação da trajetória (Figura 1).
Figura 1
Solução

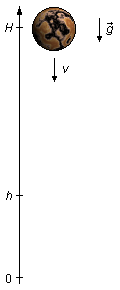
O corpo cai com a aceleração da gravidade, ele está em queda livre dado pela equação
\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_{0}+v_{0} t-\frac{g}{2} t^{2}} \tag{I} \end{gather} \]
Escrevendo a expressão (I) para a parte final do movimento
\[ \begin{gather} 0=h-v_{0 h}T-\frac{g}{2} T^{2} \tag{II} \end{gather} \]
onde v0h indica a velocidade inicial não a partir do repouso, mas a partir do ponto em que o corpo passa pelo ponto de altura h.
Para o cálculo de v0h (Figura 2), que é a velocidade que o corpo possui ao cair de H até h, \( \Delta S=h-H \), a partir do repouso, v0 = 0, como não se conhece o intervalo de tempo desta queda podemos utilizar a Equação de Torricelli para obter v0h
\[ \begin{gather} v^{2}=v_{0}^{2}-2g\Delta S \\ v_{0 h}^{2}=0^{2}-2g(h-H) \\ v_{0 h}=\sqrt{-2g (h-H)\;} \tag{III} \end{gather} \]
Figura 2

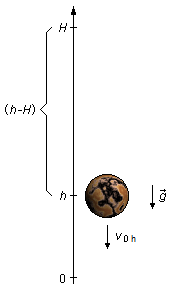
Observação: A aceleração da gravidade é maior que zero, g > 0, como h < H, temos que o espaço percorrido é menor que zero, ΔS=h−H<0, multiplicado pelo fator (−2) o termo dentro da raiz é maior que zero, portanto existe a raiz.

Substituindo a expressão (III) na expressão (II)
\[ 0=h-\sqrt{-2g (h-H)\;} T-\frac{g}{2} T^{2} \]
isolando o termo com a raiz quadrada do lado esquerdo da igualdade
\[ \sqrt{-2g (h-H)\;} T=h-\frac{g}{2}T^{2} \]
elevando os dois lados da igualdade ao quadrado
\[ \left(\sqrt{-2g (h-H)\;} T \right)^{2}=\left(h-\frac{g}{2} T^{2} \right)^{2} \]
Lembrando dos Produtos Notáveis
\[ (a-b)^{2}=a^{2}-2ab+b^{2} \]

aplicando ao termo do lado direito da igualdade
\[ -2g (h-H) T^{2}=h^{2}-2 h \frac{g}{2} T^{2}+\frac{{g}^{2}}{4} T^{4} \]
multiplicando a equação por 4
\[ \begin{gather} -4.2g (h-H) T^{2}=4h^{2}-4.2h\frac{g}{2}T^{2}+4\frac{{g}^{2}}{4}T^{4}\\ -8g (h-H) T^{2}=4h^{2}-4hgT^{2}+g^{2}T^{4} \end{gather} \]
aplicando a propriedade distributiva ao lado esquerdo da equação
\[ \begin{gather} -8ghT^{2}+8gHT^{2}=4h^{2}-4hgT^{2}+g^{2}T^{4}\\ 8gHT^{2}=4h^{2}-4hgT^{2}+g^{2}T^{2}+8ghT^{4}\\ H=\frac{4h^{2}+4hgT^{2}+g^{2}T^{4}}{8gT^{2}} \end{gather} \]
Lembrando dos Produtos Notáveis
\[ (a+b)^{2}=a^{2}+2ab+b^{2} \]

no termo do numerador fazemos as seguntes associações
\[ \begin{gather} a^{2}=4h^{2}\\ 2ab=4ghT^{2}\\ b^{2}=g^{2}T^{4} \end{gather} \]
\[ \bbox[#FFCCCC,10px] {H=\frac{(2h+gT^{2})^{2}}{8gT^{2}}} \]
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .