Um passageiro está a 5 m de distância e corre para tentar pegar um trem que está partindo do repouso com
aceleração de 2 m/s2. Qual deve ser a velocidade constante mínima do passageiro,
vp, para alcançar o trem?
Dados do problema:
- Distância do passageiro ao trem: d = 5 m;
- Velocidade inicial do trem: v0t = 0;
- Aceleração do trem: a = 2 m/s2.
Esquema do problema:
Este problema pode ser reduzido a dois pontos materiais representando o passageiro e a porta do trem.
Adotamos um sistema de referência no ponto onde se encontra o passageiro. A posição inicial do passageiro
é S0p = 0 e a posição inicial do trem é S0t = 8 m
(Figura 1).
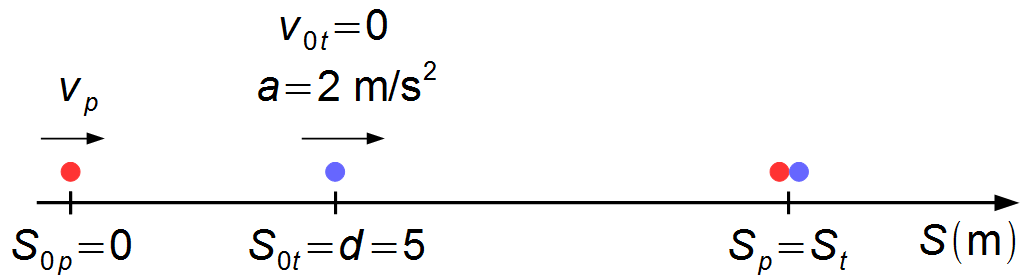
Solução:
O passageiro está correndo com velocidade constante, está em Movimento Retilíneo Uniforme
(M.R.U.), dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t}
\end{gather}
\]
\[
\begin{gather}
S_p=S_{0p}+v_pt \\[5pt]
S_p=0+v_pt \\[5pt]
S_p=v_pt \tag{I}
\end{gather}
\]
O trem está com aceleração constante, está em Movimento Retilíneo Uniformemente Variado
(M.R.U.V.), dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{S=S_0+v_0t+\frac{a}{2}t^2}
\end{gather}
\]
\[
\begin{gather}
S_t=S_{0t}+v_{0t}+\frac{a}{2}t^2 \\[5pt]
S_t=5+0\times t+\frac{a}{2}t^2 \\[5pt]
S_t=5+t^2 \tag{II}
\end{gather}
\]
Para que o passageiro alcance a porta do trem devemos impor a condição de igualdade das equações (I) e (II)
\[
\begin{gather}
S_p=S_t \\[5pt]
v_pt=5+t^2 \\[5pt]
t^2-v_pt+5=0
\end{gather}
\]
Esta é uma Equação do 2.º Grau em t.
Solução da equação
\( t^2-v_pt+5=0 \)
\[
\begin{gather}
\Delta =b^2-4ac=v_p^2-4\times 1\times 5=v_p^2-20
\end{gather}
\]
\[
\begin{gather}
t=\frac{-b\pm \sqrt{\Delta \;}}{2a}=\frac{-v_p\pm\sqrt{v_p^2-20\;}}{2\times 1}
\end{gather}
\]
Para que a equação tenha raízes reais devemos ter
\( \Delta \geqslant 0\Rightarrow v_p^2-20\geqslant 0 \)
\[
\begin{gather}
v_p^2-20\geqslant 0 \\[5pt]
v_p^2\geqslant20 \\[5pt]
v_p\geqslant\sqrt{20\;}
\end{gather}
\]
A velocidade mínima do passageiro para embarcar no trem será
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{v_p\simeq 4,5\;\mathrm{m/s}}
\end{gather}
\]
EN
ES
FR
