Exercício Resolvido de Movimento Unidimensional

De duas cidades A e B, separadas por uma distância ΔS, partem, ao nascer do Sol, um carro de cada cidade com destino a outra com velocidades constantes. Ao meio-dia eles se cruzam, o carro que partiu da cidade A chega a cidade B às 16 horas, e o carro que partiu da cidade B chega a cidade A às 21 horas. Determinar a que horas nasceu o Sol.

Dados do problema:

Distância entre as cidades: ΔS;
Instante do cruzamento entre os carros: t = 12 h;
Instante da chegada do carro de A em B: t_AB = 16 h;
Instante da chegada do carro de B em A: t_BA = 21 h;
Velocidade do carro que partiu da cidade A: v_A;
Velocidade do carro que partiu da cidade B: v_B.

Esquema do problema:

Figura 1

Solução

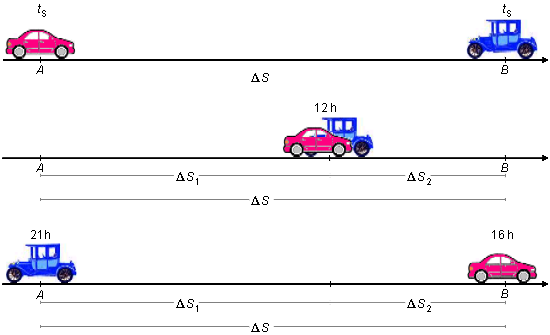
A distância total percorrida pelos carros é ΔS, dividindo este intervalo em duas partes, ΔS₁ - distância percorrida pelo carro que saiu de A até o instante do encontro com o outro carro, e, ΔS₂ - distância percorrida pelo carro que saiu de B até o encontro, temos \( \Delta S=\Delta S_{1}+\Delta S_{2} \). Os dois intervalos são diferentes, pois os carros se encontram no meio do dia (12 h), mas não no meio do caminho, eles saem de suas cidades a mesma hora (nascer do Sol), mas chegam com horários diferentes, logo suas velocidades são diferentes.
Os carros estão se movimentando com velocidade constante, estão em Movimento Retilíneo Uniforme (M.R.U.), neste tipo de movimento a velocidade média no trajeto coincide com a velocidade do móvel em qualquer ponto da trajetória, e é dada pela expressão da velocidade média

\[ \begin{gather} \bbox[#99CCFF,10px] {v_{m}=\frac{\Delta S}{\Delta t}=\frac{S_{f}-S_{i}}{t_{f}-t_{i}}} \tag{I} \end{gather} \]

Escrevendo a expressão (I) para o carro de A nos intervalos ΔS₁ e ΔS₂, e sendo t_S o instante inicial do nascer do Sol

\[ \begin{gather} v_{A}=\frac{\Delta S_{1}}{(12-t_{S})}\\[5pt] \Delta S_{1}=v_{A}(12-t_{S}) \tag{II} \end{gather} \]

\[ \begin{gather} v_{A}=\frac{\Delta S_{2}}{(16-12)}=\frac{\Delta S_{2}}{4}\\[5pt] \Delta S_{2}=4\,v_{A} \tag{III} \end{gather} \]

as expressões para o carro que parte de B serão

\[ \begin{gather} v_{B}=\frac{\Delta S_{2}}{(12-t_{S})}\\[5pt] \Delta S_{2}=v_{B} (12-t_{S}) \tag{IV} \end{gather} \]

\[ \begin{gather} v_{B}=\frac{\Delta S_{1}}{(21-12)}=\frac{\Delta S_{1}}{9}\\[5pt] \Delta S_{1}=9 v_{B} \tag{V} \end{gather} \]

As equações (II), (III), (IV) e (V) formam o seguinte sistema

\[ \begin{gather} \left\{ \begin{array}{l} \Delta S_{2}=v_{B}(12-t_{S})\\ \Delta S_{2}=4 v_{A}\\ \Delta S_{2}=v_{B}(12-t_{S})\\ \Delta S_{1}=9 v_{B} \end{array} \right. \end{gather} \]

este sistema possui quatro equações e cinco incógnitas, ΔS₁, ΔS₂, v_A, v_B e t_S, é um sistema indeterminado.
Como v_A aparece nas equações (II) e (III) podemos encontrar uma relação entre elas dividindo uma equação pela outra.

\[ \begin{gather} \frac{\Delta S_{1}}{\Delta S_{2}}=\frac{\cancel{v_{A}} (12-t_{S})}{4\cancel{v_{A}}}\\[5pt] 4 \Delta S_{1}=(12-t_{S})\Delta S_{2} \tag{VI} \end{gather} \]

Analogamente v_B aparece nas equações (IV) e (V), dividindo uma equação pela outra

\[ \begin{gather} \frac{\Delta S_{2}}{\Delta S_{1}}=\frac{\cancel{v_{B}} (12-t_{S})}{9\cancel{v_{B}}}\\[5pt] (12-t_{S})\Delta S_{1}=9 \Delta S_{2} \tag{VII} \end{gather} \]

As equações (VI) e (VII) formam um sistema de duas equações

\[ \begin{gather} \left\{ \begin{array}{l} 4 \Delta S_{1}=(12-t_{S})\Delta S_{2}\\ (12-t_{S})\Delta S_{1}=9 \Delta S_{2} \end{array} \right. \end{gather} \]

este sistema também é indeterminado, pois possui duas equações e três incógnitas, ΔS₁, ΔS₂ e t_S, dividindo a equação (VI) por (VII)

\[ \begin{gather} \frac{4 \cancel{\Delta S_{1}}}{(12-t_{S})\cancel{\Delta S_{1}}}=\frac{(12-t_{S})\cancel{\Delta S_{2}}}{9 \cancel{\Delta S_{2}}} \end{gather} \]

multiplicando em cruz

\[ \begin{gather} 4.9=(12-t_{S}).(12-t_{S})\\[5pt] 36=(12-t_{S})^{2} \end{gather} \]

Lembrando dos Produtos Notáveis \( (a-b)^{2}=a^{2}-2ab+b^{2} \)

podemos escrever a expressão do lado direito da igualdade

\[ \begin{gather} 36=144-24 t_{S}+t_{S}^{2}\\[5pt] t_{S}^{2}-24t_{S}+144-36=0\\[5pt] t_{S}^{2}-24t_{S}+108=0 \end{gather} \]

Esta é uma Equação de 2.º Grau onde a incógnita é o valor desejado t_S.

Solução da Equação de 2.º Grau \( t_{S}^{2}-24t_{S}+108=0 \)

\[ \begin{array}{l} \Delta=b^{2}-4ac=(-24)^{2}-4.1.108=576-432=144\\[10pt] t=\dfrac{-b\pm\sqrt{\Delta \,}}{2a}=\dfrac{-(-24)\pm\sqrt{144\,}}{2.1}=\dfrac{24\pm 12}{2} \end{array} \]

as duas raízes da equação serão

\[ \begin{gather} t_{S1}=18\;\text{h}\\[5pt] \qquad\text{e}\qquad\\[5pt] t_{S2}=6\;\text{h} \end{gather} \]

o horário do nascer do Sol foi às 6 h.

Observação: A solução da equação além de fornecer a hora que nasce o Sol, pedido no problema, ainda dá a hora do por do Sol às 18 h.

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .